Из вершины прямого угла \(C\) треугольника \(ABC\) проведена высота \(CP\). Радиус окружности, вписанной в треугольник \(BCP\), равен \(8\), тангенс угла \(BAC\) равен \(\frac43\). Найдите радиус окружности, вписанной в треугольник \(ABC\).
Рассмотрим чертеж (\(M, K, N\) – точки касания окружности со сторонами \(\triangle CBP\)):
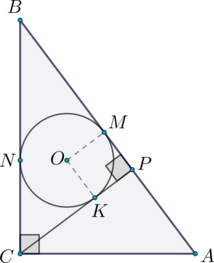
Так как \(\mathrm{tg}\,\angle BAC=\frac43\), то можно принять \(BC=4x\), \(CA=3x\). Тогда по теореме Пифагора \(AB=5x\).
Для прямоугольного треугольника с катетами \(a, b\) и гипотенузой \(c\) радиус вписанной окружности вычисляется по формуле \(0,5(a+b-c)\).
(Докажем это для \(\triangle BCP\). Так как \(OM\perp BP\), \(OK\perp CP\), то \(OMPK\) – прямоугольник. Так как \(PK=PM\) как отрезки касательных, проведенных из одной точки, то есть смежные стороны прямоугольника равны, то это квадрат. Также \(BM=BN\), \(CN=CK\) как отрезки касательных. Следовательно, если обозначить радиус вписанной окружности за \(r\), то \(a+b=BP+CP=BM+r+CK+r=(BM+CK)+2r=(BN+CN)+2r=c+2r\), откуда и вытекает нужная формула.)
Найдем \(CP\): \[\dfrac 12\cdot 4x\cdot 3x=S_{ABC}=\dfrac12\cdot CP\cdot 5x\quad\Rightarrow\quad CP=\dfrac{12}5x\] Тогда по теореме Пифагора \(BP=\frac{16}5x\). Следовательно, \[8=r_{BCP}=0,5\left(\dfrac{12}5x+\dfrac{16}5x-4x\right)\quad\Rightarrow\quad x=10\] Значит, для \(\triangle ABC\) \[r_{ABC}=0,5(4x+3x-5x)=x=10.\]
Ответ: 10



