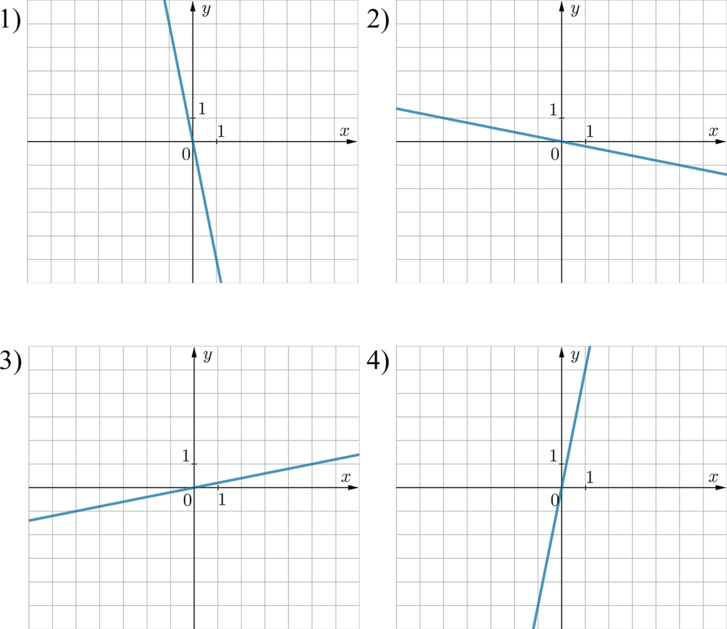
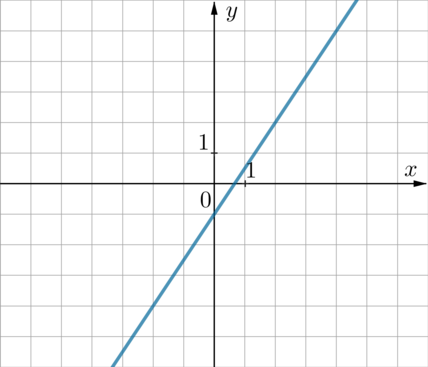
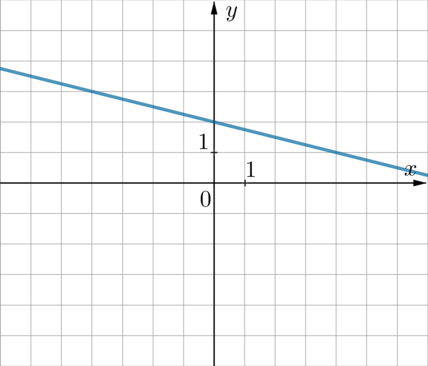
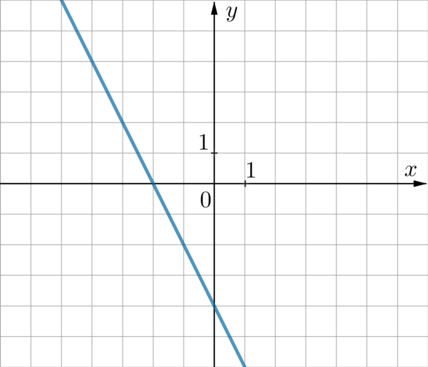
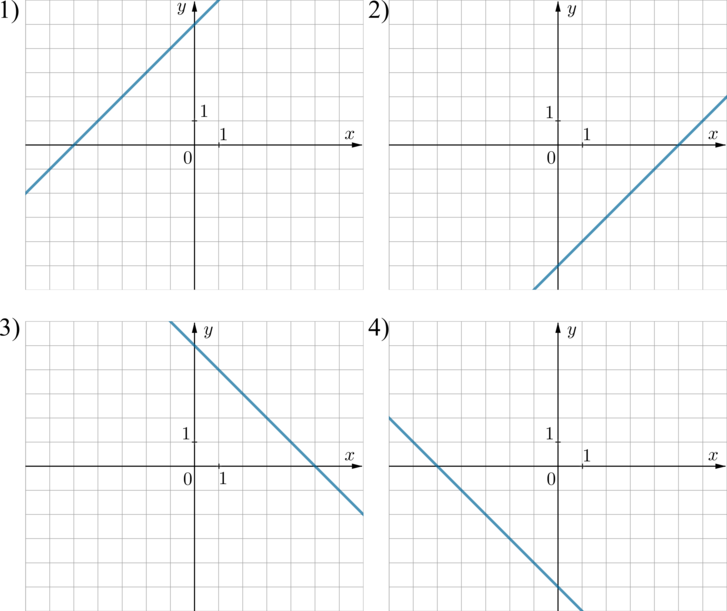
На одном из рисунков изображен график функции \(y=x-5\). Укажите номер этого рисунка.
Способ 1.
Так как уравнение прямой имеет вид \(y=x-5\), то есть коэффициент перед \(x\) положительный, то она “наклонена вправо” относительно вертикального положения. Поэтому выбираем между пунктами 1 и 2. Так как свободный коэффициент равен \(-5\), то прямая опущена на 5 единиц вниз по оси \(Oy\) относительно прямой \(y=x\) (которая проходит через начало координат). Поэтому ответ 2.
Способ 2.
Из формулы \(y=x-5\) следует, что прямая проходит, например, через точку с координатами \(x=5, y=0\). Из рисунков видно, что через эту точку проходят прямые из пунктов 2 и 3. Заметим, что прямая \(y=x-5\) также проходит через точку \(x=0, y=-5\). Среди прямых под номерами 2 и 3 через эту точку проходит только прямая 2.
Ответ: 2