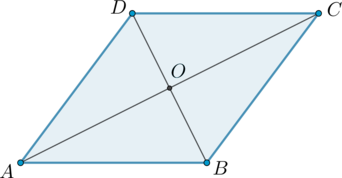
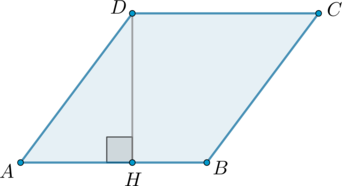
Диагонали ромба относятся как \(4:3\). Периметр ромба равен \(200\). Найдите высоту ромба.
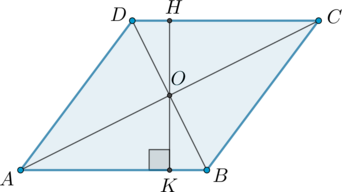
Отрезок \(HK\) – высота ромба. Так как \(AB\parallel DC\) и \(HK\perp AB\), то \(HK\perp DC\).
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника, а у равных треугольников высоты, опущенные к равным сторонам, равны, то \(OK=OH\).
Рассмотрим \(\triangle AOB\). Так как \(AC:BD=4:3\), то также \(AO:BO=4:3\). Пусть \(AO=4x, BO=3x\). Следовательно, \(AB=\sqrt{(4x)^2+(3x)^2}=5x\).
Так как у ромба все стороны равны, то его сторона равна \(200:4=50\), следовательно, \(5x=50\) и \(x=10\).
Высота прямоугольного треугольника \(AOB\), опущенная из вершины прямого угла \(O\), равна \(AO\cdot OB:AB\), следовательно, \[OK=\dfrac{4x\cdot 3x}{5x}=\dfrac{12}5x=24\quad\Rightarrow\quad HK=24\cdot 2=
48\]
Ответ: 48