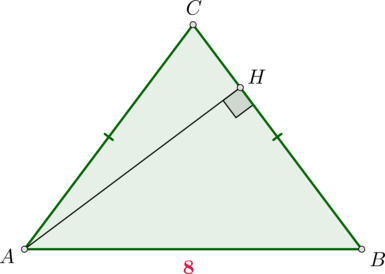
В треугольнике \(ABC\) известно, что \(AC=BC=4\sqrt{15}\), \(\sin\angle BAC=0,25\). Найдите высоту \(AH\).
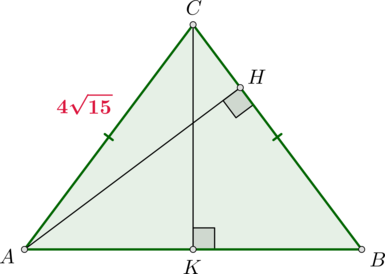
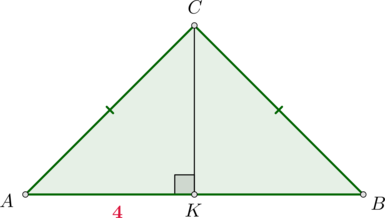
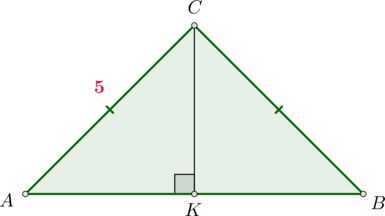
Так как \(\triangle ABC\) равнобедренный, то \(\angle BAC=\angle ABC\), следовательно, \(\sin\angle ABC=\sin\angle BAC=0,25\). Следовательно, из \(\triangle AHB\): \[\dfrac{AH}{AB}=\sin\angle ABC=\dfrac14 \quad\Rightarrow\quad AH=\dfrac14AB\] Проведем \(CK\perp AB\). Тогда \(CK\) также является медианой. Из \(\triangle CKB\): \[\dfrac{CK}{BC}=\sin\angle ABC=\dfrac14\quad\Rightarrow\quad CK=\sqrt{15}\] Следовательно, по теореме Пифагора из \(\triangle CKB\): \[KB=\sqrt{BC^2-CK^2}=\sqrt{(4\sqrt{15})^2-(\sqrt{15})^2}= \sqrt{3\sqrt{15}\cdot 5\sqrt{15}}=15\] Следовательно, \(AB=2KB=30\) и \(AH=\frac14AB=7,5\).
Ответ: 7,5