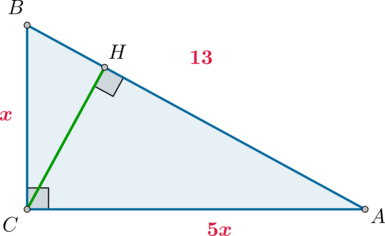
В треугольнике \(ABC\) угол \(C=90^\circ\), \(CH\) – высота, \(AB=26\), \(\mathrm{tg}\,\angle B=5\). Найдите \(AH\).
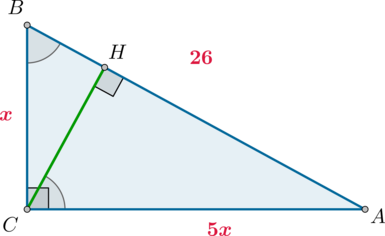
По определению из \(\triangle ABC\): \[\dfrac{AC}{BC}=\mathrm{tg}\,\angle B=\dfrac 51\] Следовательно, можно принять \(AC=5x\), \(BC=x\). Тогда по теореме Пифагора \(x^2+(5x)^2=26^2\), откуда \(x=\sqrt{26}\).
Тогда \[\sin\angle B=\dfrac{AC}{AB}=\dfrac5{\sqrt{26}}\] По свойству прямоугольного треугольника \(\angle B=\angle HCA\). Следовательно, из \(\triangle HCA\): \[\dfrac5{\sqrt{26}}=\sin \angle HCA=\dfrac{AH}{AC}\quad\Rightarrow\quad
AH=25\]
Ответ: 25