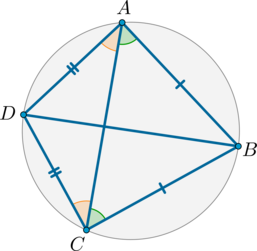
Хорды \(KN\) и \(LM\) взаимно перпендикулярны. Найдите угол \(NLM\), если угол \(KML\) равен \(35^\circ\). Ответ дайте в градусах.
Рассмотрим картинку:
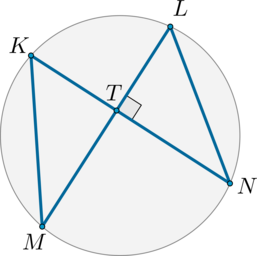
Вписанные углы \(KML\) и \(KNL\) опираются на одну и ту же дугу, следовательно, они равны, значит, \(\angle KNL=35^\circ\). Тогда \(\angle NLM=180^\circ-90^\circ-35^\circ=55^\circ\).
Ответ: 55