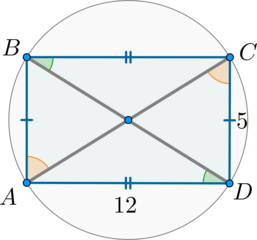
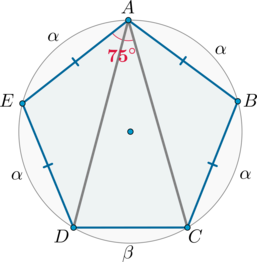
Рассмотрим картинку:
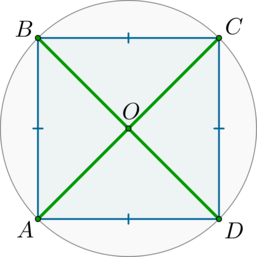
Докажем, что данный четырехугольник является квадратом.
Т.к. хорды \(AB\) и \(CD\) равны, то равны дуги \(\buildrel\smile\over{AB}\) и \(\buildrel\smile\over{CD}\). Следовательно, вписанные углы, опирающиеся на эти дуги, будут тоже равны:
\[\angle ADB=\angle ACB=\angle DAC=\angle DBC\]
Таким образом, \(\angle ADB=\angle DBC\) – накрест лежащие при прямых \(AD\) и \(BC\) и секущей \(BD\), следовательно, \(AD\parallel BC\).
Аналогичным образом доказывается, что \(AB\parallel CD\).
Таким образом, \(ABCD\) – параллелограмм. Т.к. он вписанный, то это – прямоугольник. Т.к. все его стороны равны, то это квадрат.
В квадрате центр описанной окружности лежит на пересечении диагоналей, следовательно, \(AC=2R=6\). По свойству квадрата \(AD=AC\div \sqrt2=3\sqrt2\). Следовательно, площадь
\[S_{ABCD}=AD^2=(3\sqrt2)^2=18.\]
Замечание.
Можно было доказать, что \(ABCD\) – квадрат, другим способом:
\(\triangle ABD=\triangle CBD\) по трем сторонам. Следовательно, \(\angle A=\angle C\). Но т.к. четырехугольник вписанный, то сумма противоположных углов равна \(180^\circ\), следовательно, \(\angle
A+\angle C=180^\circ\). Отсюда следует, что \(\angle A=\angle
C=90^\circ\). Аналогично \(\angle B=\angle D=90^\circ\). По признаку четырехугольник, у которого все углы прямые, является прямоугольником. Но т.к. у него еще и все стороны равны, то это квадрат.
Ответ: 18