Треугольники \(ABC\) и \(ADC\) имеют равные углы \(B\) и \(D\), причем отрезок \(BD\) не пересекает прямую \(AC\). Найдите угол \(DAC\), если угол \(DBC\) равен \(60^\circ\). Ответ дайте в градусах.
Учитывая условие, рисунок будет выглядеть так:
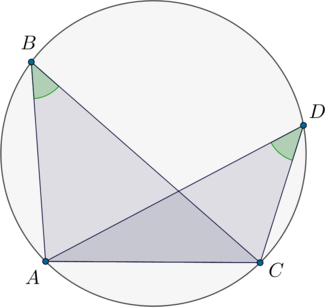
По признаку четырехугольник \(ABDC\) является вписанным, то есть около него можно описать окружность. Следовательно, \(\angle DAC=\angle
DBC=60^\circ\) как вписанные углы, опирающиеся на одну дугу.
Заметим, что фраза “отрезок не пересекает прямую” абсолютно не значит, что отрезок и прямая параллельны! Вот если бы это было сказано о двух прямых – другое дело. Если бы отрезок пересекал прямую, то картинка выглядела бы, например, так:
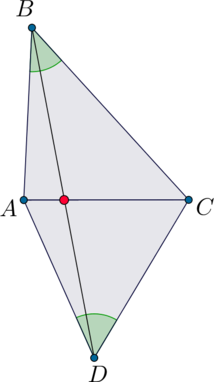
Ответ: 60



