Теоремы, связанные с длинами отрезков (страница 2)

Произведение отрезков одной из пересекающихся хорд равно произведению отрезков другой. Покажем это:
Соединим \(AC\) и \(BD\)



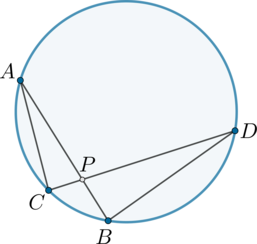
Рассмотрим треугольники \(APC\) и \(PBD\):
\(\angle APC = \angle BPD\), как вертикальные,
\(\angle ACD\) и \(\angle ABD\) – вписанные, опирающиеся на одну дугу, следовательно, \(\angle ACD = \angle ABD\).

Таким образом, треугольники \(APC\) и \(PBD\) – подобны по двум углам. Из их подобия следует, что \[\dfrac{CP}{PB} = \dfrac{AP}{PD}\] (в подобных треугольниках против равных углов лежат пропорциональные стороны), откуда можно получить \(CP \cdot PD = AP \cdot PB\).
В данной задаче имеем: \(3 \cdot PD = 6 \cdot 4\), откуда \(PD = 8\).

Ответ: 8

Квадрат отрезка касательной равен произведению отрезков секущей: \(AP^2 = PB \cdot PC\). Покажем это:
Соединим \(AB\) и \(AC\)



Рассмотрим треугольники \(APB\) и \(APC\):
\(\angle APC\) – общий,
Так как угол между касательной и хордой равен половине градусной меры дуги окружности, заключённой внутри него, то \(\angle PAB = 0,5\cdot \buildrel\over{AB} = \angle ACB\).

Таким образом, треугольники \(APC\) и \(APB\) – подобны по двум углам. Из их подобия следует, что \[\dfrac{AP}{PC} = \dfrac{PB}{AP}\] (в подобных треугольниках против равных углов лежат пропорциональные стороны), откуда можно получить \(AP^2 = PB \cdot PC\).
В данной задаче имеем: \(16 = PB \cdot 8\), откуда \(PB = 2\).

Ответ: 2

Произведение отрезков секущих равны: \(AB \cdot AC = AD \cdot AE\). Покажем это:
Построим \(AF\) – касательную



Так как квадрат отрезка касательной равен произведению отрезков секущей, то \(AB \cdot AC = AF^2 = AD \cdot AE\).
В данной задаче имеем: \(18 = 2 \cdot AE\), откуда \(AE = 9\), тогда \(DE = AE - AD = 9 - 2 = 7\).

Ответ: 7

Отрезки касательных, проведённых из одной точки, равны: \(AB = AC\). Покажем это: Построим радиусы \(OB\) и \(OC\) и соединим \(OA\)

Так как радиус, проведённый в точку касания, перпендикулярен касательной, то \(\angle ACO = 90^{\circ} = \angle ABO\).
\(OC = OB\), как радиусы, тогда
в прямоугольных треугольниках \(AOC\) и \(AOB\) катеты \(OC\) и \(OB\) равны, а гипотенуза \(AO\) – общая, следовательно, треугольники \(AOC\) и \(AOB\) равны по катету и гипотенузе, откуда получаем \(AB = AC\).

Таким образом, треугольник \(ABC\) – равнобедренный и \[\angle ACB = \angle ABC = 0,5(180^{\circ} - \angle CAB) = 61^{\circ}.\]

Ответ: 61

Равные дуги стягивают равные хорды: \(DC = AB\). Покажем это:
Построим радиусы \(OC\) и \(OA\)

Так как дуги \(CD\) и \(AB\) равны, то их градусные меры совпадают, тогда \(\angle COD = \angle AOB\), как центральные углы, опирающиеся на равные дуги.
\(CO = OD = AO = OB\), как радиусы, тогда
треугольники \(AOB\) и \(DOC\) равны по двум сторонам и углу между ними, следовательно, \(DC = AB\).
\(QD = QC + CD = QA + AB\), тогда треугольник \(QBD\) – равнобедренный и \(63^{\circ} = \angle QBD = \angle QDB\), значит \[\angle BQD = 180^{\circ} - 63^{\circ} - 63^{\circ} = 54^{\circ}.\]

Ответ: 54