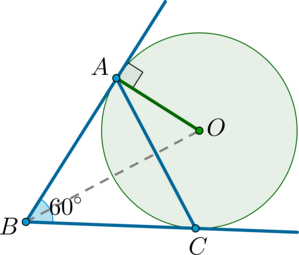
Окружность вписана в угол \(B\), равный \(60^\circ\). Найдите расстояние от вершины угла до центра этой окружности, если расстояние между точками касания окружности и сторон угла равно \(2\sqrt3\).
Обозначим точки касания окружности и сторон угла за \(A\) и \(C\). Тогда известно, что \(AC=2\sqrt3\). Пусть также \(O\) – центр окружности. То есть необходимо найти \(OB\).
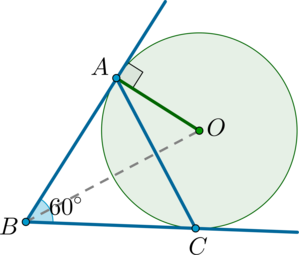
\(OA\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).
Рассмотрим \(\triangle ABC\): он равнобедренный (\(AB=BC\) как отрезки касательных, проведенных из одной точки), следовательно, \(\angle A=\angle C=0,5\cdot(180^\circ-60^\circ)=60^\circ\). Таким образом, он равносторонний, следовательно, \(AB=AC=2\sqrt3\).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=30^\circ\). Тогда из прямоугольного \(\triangle ABO\):
\[\cos 30^\circ=\dfrac{BA}{OB}=\dfrac{2\sqrt3}{OB} \quad \Rightarrow \quad OB=2\sqrt3\cdot \dfrac2{\sqrt3}=4.\]
Ответ: 4