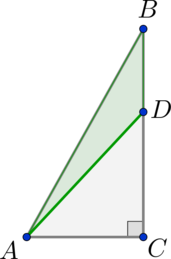
Сторона \(AB\) треугольника \(ABC\) равна \(2\), его периметр \(P = 9\), а его площадь равна \(\dfrac{\sqrt{135}}{4}\), причём \(AC\cdot BC = 12\). Найдите \(BC + AC\).

По формуле Герона \(S_{\triangle ABC} = \sqrt{p(p - AB)(p - BC)(p - AC)}\), где \(p\) – полупериметр треугольника \(ABC\), \(p = 4,5\),
тогда \(S_{\triangle ABC}^2 = p(p - AB)(p - BC)(p - AC)\), тогда \(\dfrac{S_{\triangle ABC}^2}{p(p - AB)} = (p - BC)(p - AC) =
p^2 - p(AC + BC) + AC\cdot BC\), откуда
\(\dfrac{\frac{135}{16}}{4,5\cdot 2,5} = \dfrac{81}{4} - \dfrac{9}{2}(AC + BC) + 12\qquad\Rightarrow\qquad \dfrac{135}{16} \cdot\dfrac{4}{45} = \dfrac{81}{4} - \dfrac{9}{2}(AC + BC) + 12\qquad\Rightarrow\)
\(\Rightarrow\qquad \dfrac{39}{2} = \dfrac{9}{2}(AC + BC) - 12 \qquad\Rightarrow\qquad AC + BC = 7.\)
Ответ: 7