Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Боковая сторона треугольника равна \(20\). Найдите площадь этого треугольника.

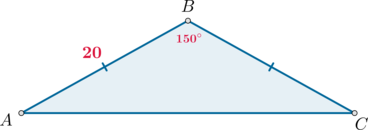
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 20^2 \cdot \dfrac12=100\]
Ответ: 100