Площадь параллелограмма, ромба, прямоугольника и квадрата (страница 3)

Так как площадь ромба равна половине произведения диагоналей, то \[S=0,5\cdot 4\cdot 12=24\]

Ответ: 24

Проведем \(DH\perp AB\).



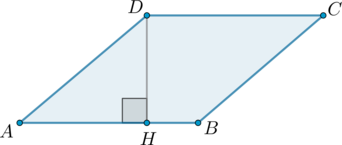
Так как \(\angle A=30^\circ\), а катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(AD=2DH=2\cdot 2=4\). Площадь ромба равна произведению высоты на сторону, к которой проведена высота, следовательно, \[S=DH\cdot AB=4\cdot 2=8\] (\(AB=AD\), так как в ромбе по определению все стороны равны)

Ответ: 8

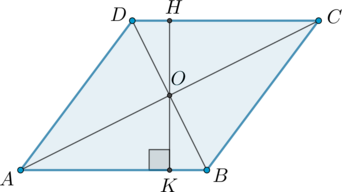
Отрезок \(HK\) – высота ромба. Так как \(AB\parallel DC\) и \(HK\perp AB\), то \(HK\perp DC\).

Так как у ромба все стороны равны, то его сторона равна \(AB=200:4=50\). Следовательно, площадь ромба равна \(S=50HK\) (произведение стороны на высоту, проведенную к этой стороне).
Так как \(AC:BD=4:3\), то можно принять \(AC=4a, BD=3a\). Так как площадь ромба равна полупроизведению диагоналей, то \(S=0,5\cdot 4a\cdot 3a=6a^2\), следовательно, \[50HK=6a^2\quad\Rightarrow\quad HK=\dfrac3{25}a^2\] Так как диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, то по теореме Пифагора из \(\triangle AOB\): \[\left(\dfrac32a\right)^2+(2a)^2=AB^2\quad\Rightarrow\quad a^2=400\] Следовательно, \[HK=\dfrac3{25}\cdot 400=48\]

Ответ: 48

Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена: \(S=ah\). Тогда \(h=S:a\). Следовательно, чем больше \(a\), тем меньше \(h\) (при фиксированном \(S\)). Таким образом, большая высота равна \[h=\dfrac{40}5=8\]

Ответ: 8