18. Площади геометрических фигур
В треугольнике \(KDA\) проведена медиана \(DB = 3\). Найдите площадь треугольника \(KDA\), если известно, что \(KD = 4, KA = 10\).
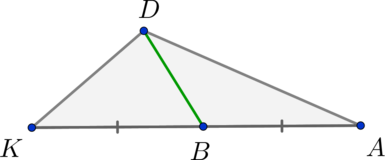
Медиана \(DB\) делит \(KA\) пополам \(\Rightarrow KB = 5\). Так как известны все стороны треугольника \(KDB\), найдем его площадь по формуле Герона: \[S_{KDB} = \sqrt{6\cdot(6 - 3)(6 - 4)(6 - 5)}=6.\] Медиана треугольника делит его на два равновеликих треугольника, то есть \(S_{KDB}=S_{ADB}\), следовательно,
\[S_{KDA} = 2\cdot S_{KDB} = 12.\]
Ответ: 12
В прямоугольном треугольнике \(ABC\) с прямым углом \(C\) проведена биссектриса \(BT\), причем \(AT = 15, TC = 12\). Найдите площадь треугольника \(ABT\).
По свойству биссектрисы: \[\dfrac{TC}{BC} = \dfrac{AT}{AB}\] Пусть \(BC = x, AB = y\), тогда: \[\dfrac{12}x = \dfrac{15}y\Rightarrow x = 0,8\cdot y.\] Из треугольника \(ABC\) имеем по теореме Пифагора: \(x^2+27^2 =
y^2\Rightarrow 0,64\cdot y^2 + 27^2 = y^2\Rightarrow y = 45, x =
36.\) \[S_{ABT} = 0,5\cdot AT\cdot BC = 0,5\cdot 15\cdot 36 = 270.\]
Ответ: 270
Площадь равнобедренного треугольника \(ABC\) равна \(90\), боковая сторона равна \(10\sqrt{3}\). К основанию \(AB\) и стороне \(BC\) проведены высоты \(CP\) и \(AH\), пересекающиеся в точке \(D\). Найдите площадь треугольника \(CDH\).
Так как треугольник \(ABC\) равнобедренный, то \(CA = CB=10\sqrt3\), следовательно, \(S_{ABC} = 0,5\cdot CB\cdot AH =
90\quad\Rightarrow\quad AH = 6\sqrt{3}\).
Из треугольника \(HCA\) по теореме Пифагора имеем: \(CH = \sqrt{CA^2 -
AH^2} = 8\sqrt{3}.\)
Так как \(CP\) — высота равнобедренного треугольника \(ABC\), проведенная к основанию \(AB\), то она также является биссектрисой и медианой. Тогда по свойству биссектрисы из \(\triangle HCA\): \[\dfrac{DH}{CH} = \dfrac{DA}{CA} \quad\Rightarrow \quad
\dfrac{DH}{8\sqrt{3}} =\dfrac{(6\sqrt{3} -
DH)}{10\sqrt{3}}\quad\Rightarrow \quad DH = \dfrac{8\sqrt{3}}3\] Следовательно, так как \(\triangle CDH\) прямоугольный, то \(S_{CDH} =
0,5\cdot CH\cdot DH = 32.\)
Ответ: 32
Площадь равнобедренного треугольника \(ABC\) с основанием \(AC\) равна \(20\). В нем проведены высоты \(BD\) и \(AH\), пересекающиеся в точке \(L\). Найдите площадь треугольника \(BLH\), если \(AH = 4\sqrt{2}\).
\[S_{ABC} = 0,5\cdot AH\cdot CB = 20\quad\Rightarrow \quad CB =5\sqrt{2}.\] Так как треугольник \(ABC\) равнобедренный с основанием \(AC\), то \(AB=CB=5\sqrt2\).
Из треугольника \(ABH\) по теореме Пифагора:
\[HB = \sqrt{AB^2 - AH^2} = 3\sqrt{2}.\] Так как \(BD\) — высота равнобедренного треугольника \(ABC\), проведенная к основанию, то она также является биссектрисой и медианой. Тогда по свойству биссектрисы из \(\triangle ABH\):
\[\dfrac{HL}{HB} = \dfrac{AH-HL}{AB}\quad \Rightarrow\quad HL = 1,5\sqrt{2}.\] Следовательно, \(S_{BLH} = 0,5\cdot HL\cdot HB = 4,5.\)
Ответ: 4,5
Найдите квадрат площади треугольника со сторонами \(7\), \(11\) и \(6\sqrt6\).
По формуле Герона квадрат площади треугольника равен
\(S^2=\dfrac{7+11+6\sqrt6}2\cdot \left(\dfrac{7+11+6\sqrt6}2-6\sqrt6\right)\cdot \left(\dfrac{7+11+6\sqrt6}2-7\right) \cdot \left( \dfrac{7+11+6\sqrt6}2-11\right)=\)
\(=\dfrac{7+11+6\sqrt6}2\cdot \dfrac{7+11-6\sqrt6}2\cdot \dfrac{11+6\sqrt6-7}2\cdot \dfrac{7+6\sqrt6-11}2=\)
\(=\dfrac1{16}\cdot (18+6\sqrt6)(18-6\sqrt6)(6\sqrt6+4)(6\sqrt6-4)=\)
\(=\dfrac1{16}\cdot 6^2\cdot (3+\sqrt6)(3-\sqrt6)\cdot ((6\sqrt6)^2-4^2)=\dfrac{6^2\cdot 3\cdot 200}{16}=1350\).
Ответ: 1350
У треугольника со сторонами \(9\) и \(6\) проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна \(4\). Чему равна высота, проведенная ко второй стороне?
Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне. Следовательно, с одной стороны, \(S=0,5\cdot 9\cdot 4\), а с другой стороны \(S=0,5\cdot 6\cdot h\), где \(h\) – высота, которую нужно найти. Следовательно, \[0,5\cdot 9\cdot 4=0,5\cdot 6\cdot h\quad\Leftrightarrow\quad h=6\]
Ответ: 6
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Боковая сторона треугольника равна \(10\). Найдите площадь этого треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 10^2 \cdot \dfrac12=25\]
Ответ: 25
