Проектор полностью освещает экран В высотой 160 см, расположенный на расстоянии 300 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран А высотой 80 см. чтобы он был полностью освещен, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
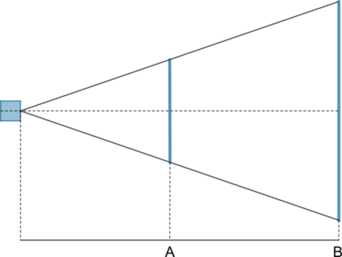
Расстояние от проектора до экрана – это перпендикуляр. Следовательно, можно рассмотреть два прямоугольных треугольника \(QWE\) и \(QRT\):
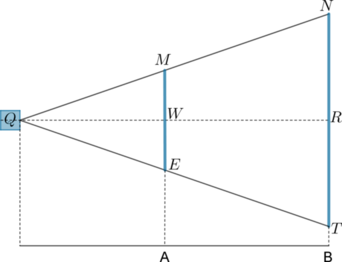
Заметим, что треугольники \(QME\) и \(QNT\) равнобедренные, поэтому \(WE=\frac{1}{2} ME=40 \) см и \(RT=\frac{1}{2}NT=80\) см. Из условия следует, что \(QR=300\) см.
Треугольники \(QWE\) и \(QRT\) подобны по двум углам, поэтому \(\frac{QW}{QR}=\frac{WE}{RT}\). По свойству пропорции \(QW=\frac{WE}{RT}\cdot QR=\frac{40 \cdot 300}{80} = 150\).
Ответ: 150



