Задачи на движение по прямой (страница 3)

Изобразим в виде схемы движение велосипедиста:

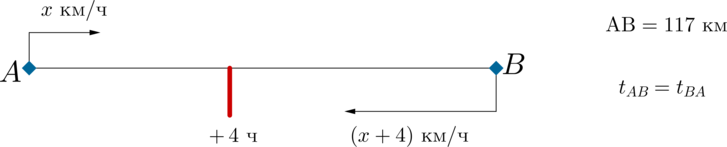
Время в часах, которое он затратил на дорогу из A в B, равно \[t_{AB}=\dfrac{117}x\] Время в часах, которое он затратил на дорогу из В в А, учитывая остановку, равно \[t_{BA}=4+\dfrac{117}{x+4}\] Так как \(t_{AB}=t_{BA}\), то получаем уравнение: \[\dfrac{117}x=4+\dfrac{117}{x+4}\] Домножим обе части уравнения на \(x(x+4)\), так как \(x\ne 0, \ x+4\ne 0\) – скорости. \[117(x+4)=4x(x+4)+117x \quad\Leftrightarrow\quad 117x+117\cdot 4=4(x^2+4x)+117x \quad\Leftrightarrow\quad 4(x^2+4x)-117\cdot 4=0 \quad\Leftrightarrow\quad x^2+4x-117=0\] Дискриминант \(D=4^2+117\cdot 4=4(4+117)=4\cdot 121=(2\cdot 11)^2\), следовательно, корни уравнения \(x_1=-13\) и \(x_2=9.\) Так как скорость не может быть отрицательной, то \(x=9\). Тогда скорость велосипедиста на пути из В в А равна \(x+4=13\).

Ответ: 13

Рассмотрим схематичный рисунок:



Условно назовем паром, отчаливший от левого берега, зеленым, а паром, отчаливший от правого – синим. Пусть скорость зеленого \(x\) км/ч, синего \(y\) км/ч.
Из условия задачи следует, что \(AC=0,9\) км, \(BD=0,3\) км.
Пусть \(BC=S\). Тогда \(AB=AC+BC=0,9+S\). Так как до первой встречи паромы двигались одинаковое количество времени, то можно составить равенство: \[\dfrac Sy=\dfrac {0,9}x \quad\Rightarrow\quad \dfrac xy=\dfrac{0,9}S\]

После первой встречи и до второй встречи синий прошел расстояние, равное \(AC+AD=AC+(AB-BD)=0,9+0,9+S-0,3=1,5+S\), а зеленый – равное \(BC+BD=S+0,3\). Время, потраченное на путь у каждого парома, также было одинаковым. Следовательно, можно составить второе равенство: \[\dfrac{1,5+S}y=\dfrac{S+0,3}x \quad\Rightarrow\quad \dfrac xy=\dfrac{S+0,3}{1,5+S}\]

Таким образом, из полученных двух равенств можно заключить: \[\dfrac{0,9}S=\dfrac{S+0,3}{1,5+S} \quad\Rightarrow\quad S^2-0,6S-0,9\cdot 1,5=0\]

По теореме Виета корнями уравнения будут числа \(-0,9\) и \(1,5\). Так как \(S\) – длина отрезка, то есть неотрицательная величина, то \(S=1,5\). Следовательно, ширина реки равна \(AB=1,5+0,9=2,4\).

Ответ: 2,4

Из картинки видно, что “поезд проходит мимо столба” – это то же самое, что “поезд проходит расстояние, равное длине поезда”, а “поезд проходит через туннель” – это то же самое, что “поезд проходит расстояние, равное длине поезда плюс длине туннеля”.
Следовательно, так как длина поезда 1 км, а мимо столба он проходит за 1 мин, то его скорость равна 1 км/мин. Следовательно, 1 км/мин \(\cdot\) 3 мин \(=\) 3 км – длина поезда плюс длина туннеля. Следовательно, длина туннеля равна 2 км.

Ответ: 2

Заметим, что фраза “первый поезд прошел мимо пассажира за 12 с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12 с. Следовательно, неважно, где именно в поезде в этот момент находился пассажир. Поэтому пусть пассажир находился прямо в начале поезда.



Первая картинка – когда пассажир увидел голову поезда, вторая – хвост поезда.
Заметим, что за каждую секунду первый поезд проезжает \(\dfrac{70000}{3600}=\dfrac{175}9\) м, второй – \(\dfrac{80000}{3600}=\dfrac{200}9\) м.

Следовательно, за каждую секунду пассажир удаляется от головы первого поезда на \(\dfrac{175}9+\dfrac{200}9=\dfrac{125}3\) м. Следовательно, через 12 с он удалится от головы поезда на \(\dfrac{125}3\cdot 12=500\) м. Так как в этот момент он будет видеть хвост поезда, то это значит, что 500 м и есть длина первого поезда.

Ответ: 500

Заметим, что так как впереди находится второй (медленный) автомобиль, то сначала автомобили будут сближаться (до того момента, как первый догонит второго), а затем будут удаляться.
Так как расстояние между ними в начале движения 36 км и \(36>21\), то первый раз расстояние в 21 км между ними будет, пока они сближаются, а второй раз – когда они будут отдаляться.



Скорость сближения автомобилей равна \(46-40=6\) км/ч. Расстояние между ними должно измениться с 36 км до 21 км, то есть на \(36-21=15\) км. Следовательно, первый раз это произойдет через \(15:6=2,5\) часа.
Теперь найдем, через сколько часов после начала движения первый догонит второго. Это значит, что расстояние между ними должно стать равным 0 км. Значит, должно измениться на 36 км. Следовательно, время встречи равно \(36:6=6\) часов.
Значит, спустя 6 часов движения картинка выглядит так:



Скорость отдаления также равна 6 км/ч. Расстояние между ними должно измениться с 0 км до 21 км, следовательно, на 21 км, следовательно, это произойдет через \(21:6=3,5\) часа после встречи. Значит, второй раз расстояние между ними будет равно 21 км через \(6+3,5=9,5\) часов.
Так как в задаче два ответа, то в бланк мы запишем \(2,5+9,5=12\)

Ответ: 12

Заметим, что так как более быстрый мотоциклист находится впереди, то расстояние между мотоциклистами будет только увеличиваться (то есть они будут только отдаляться друг от друга). Значит, в задаче будет только один ответ.
Следовательно, расстояние между ними должно измениться на \(17,5-10=7,5\) км (так как изначально они находились на расстоянии 10 км друг от друга). Скорость удаления мотоциклистов равна \(31-16=15\) км/ч. Следовательно, время, через которое расстояние между ними увеличится еще на 7,5 км, равно \(7,5:15=0,5\) часа или \(30\) минут.

Ответ: 30

Пусть \(x\) км/ч – скорость быстрого (следовательно, \(x>10\)). Тогда \(x-10\) км/ч – скорость, с которой быстрый удаляется от медленного. Значит, за 6 часов он удалится от медленного на \(6\cdot(x-10)\) км, следовательно, \(6(x-10)=48\), откуда \(x=18\).



За 3,5 ч медленный пройдет 35 км, следовательно, если быстрому нужно отъехать назад на \(s\) км, то он должен за 3,5 ч пройти \(s+35\) км. Следовательно, \(18\cdot 3,5=s+35\), откуда \(s=28\).

Ответ: 28