На клетчатой бумаге с размером клетки \(1\times1\) изображен ромб. Найдите его площадь.

Проведем диагонали данного ромба:
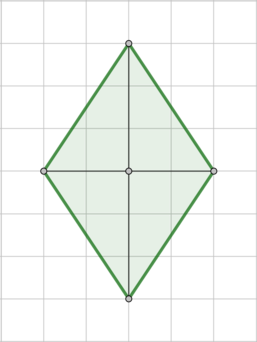
Площадь ромба равна полупроизведению диагоналей, следовательно, \[S=\dfrac12\cdot 4\cdot 6=12\]
Ответ: 12
19. Задачи на клетчатой бумаге
На клетчатой бумаге с размером клетки \(1\times1\) изображен ромб. Найдите его площадь.

Проведем диагонали данного ромба:

Площадь ромба равна полупроизведению диагоналей, следовательно, \[S=\dfrac12\cdot 4\cdot 6=12\]
Ответ: 12
Найдите радиус окружности, вписанной в треугольник \(ABC\), считая стороны квадратных клеток равными \(1\).
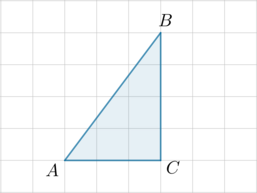
Так как радиус окружности, вписанной в прямоугольный треугольник, ищется по формуле \(r=(a+b-c):2\), где \(a, b\) – катеты, \(c\) – гипотенуза, то \[r=\dfrac{3+4-\sqrt{3^2+4^2}}2=1\]
Ответ: 1
На клетчатой бумаге с размером клетки \(1\times1\) изображен равнобедренный прямоугольный треугольник. Найдите длину его высоты, выходящей из вершины прямого угла.

Так как треугольник равнобедренный, то высота, проведенная к гипотенузе-основанию, является также медианой. По свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У данного прямоугольного треугольника гипотенуза равна \(5\). Следовательно, медиана (она же высота) равна \(2,5\).
Ответ: 2,5
На клетчатой бумаге с размером клетки \(1\times1\) изображен равнобедренный прямоугольный треугольник. Найдите длину его биссектрисы, выходящей из вершины прямого угла.

Так как треугольник равнобедренный, то биссектриса, проведенная к гипотенузе-основанию, является также медианой. По свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У данного прямоугольного треугольника гипотенуза равна \(5\). Следовательно, медиана (она же биссектриса) равна \(2,5\).
Ответ: 2,5
На клетчатой бумаге с размером клетки \(1\times1\) изображен равнобедренный прямоугольный треугольник. Найдите радиус описанной около него окружности.

Центр окружности, описанной около прямоугольного треугольника, лежит в середине его гипотенузы, то есть радиус этой окружности равен половине гипотенузы. У данного прямоугольного треугольника гипотенуза равна \(5\). Следовательно, радиус равен \(2,5\).
Ответ: 2,5
На клетчатой бумаге с размером клетки \(1\times1\) изображен угол. Найдите его градусную величину.
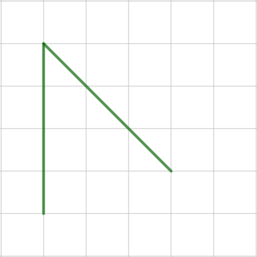
Отметим точки \(A, B, C, D\) и рассмотрим прямоугольный \(\triangle ABC\):
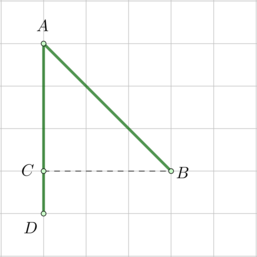
\(AC=BC=3\) – катеты, следовательно, треугольник равнобедренный, значит, \[\angle BAD=\angle BAC=45^\circ\]
Ответ: 45
На клетчатой бумаге с размером клетки \(1\) см \(\times\) \(1\) см отмечены точки \(A\) и \(B\). Найдите длину отрезка \(AB\) в сантиметрах.

Рассмотрим прямоугольный \(\triangle ABC\):
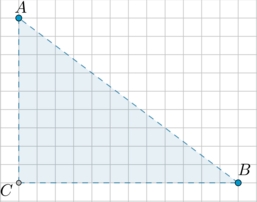
Катеты \(AC\) и \(BC\) равны соответственно \(9\) и \(12\), следовательно, по теореме Пифагора гипотенуза \(AB\) равна \[AB=\sqrt{9^2+12^2}=15\]
Ответ: 15