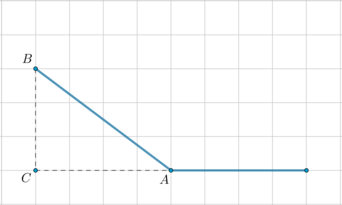
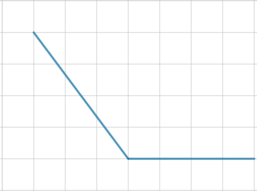
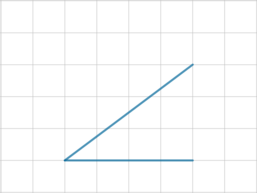
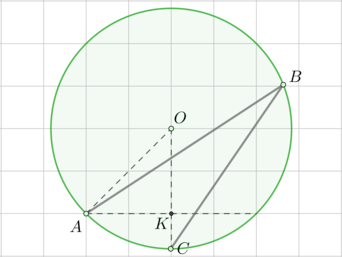
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки \(1\) см \(\times\) \(1\) см. Ответ дайте в квадратных сантиметрах.
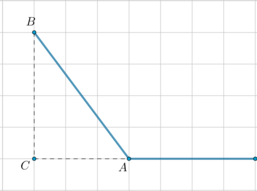
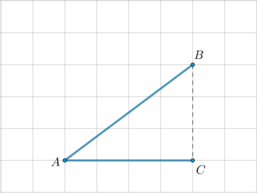
Отметим точки \(A, B, C\) и проведем отрезок \(CH\), как показано на рисунке:
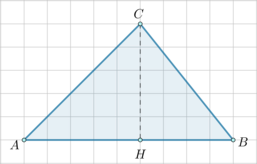
Заметим, что \(CH\perp AB\). Следовательно, площадь треугольника равна \[S=\dfrac12\cdot AB\cdot CH=\dfrac12\cdot 9\cdot 5=22,5\]
Ответ: 22,5