Найдите угол \(ABC\). Ответ дайте в градусах.

Пусть \(O\) – центр окружности.
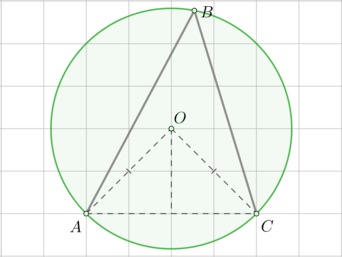
Пусть сторона клетки равна \(1\). Точки \(O\), \(C\) и \(A\) находятся в узлах решетки, причем \(AO\) – гипотенуза равнобедренного прямоугольного треугольника с катетами \(2\), следовательно, \(AO=2\sqrt2\). \(AO=CO\) – радиусы окружности. \(AC=4\).
Заметим, что \(AO^2+CO^2=AC^2\), следовательно, по обратной теореме Пифагора, \(\angle AOC=90^\circ\). Это центральный угол, опирающийся на хорду \(AC\). Тогда вписанный угол \(ABC\), опирающийся на эту же хорду, равен половине \(\angle AOC\), то есть \(45^\circ\).
Ответ: 45



