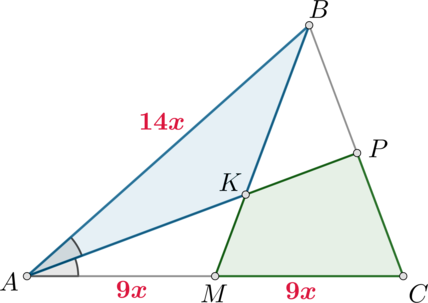
В треугольнике \(ABC\) на его медиане \(BM\) отмечены точка \(K\) так, что \(BK:KM=4:1\). Прямая \(AK\) пересекает сторону \(BC\) в точке \(P\). Найдите отношение площади треугольника \(ABK\) к площади четырехугольника \(KPCM\).

Показать решение

Так как медиана треугольника делит его на два треугольника, равных по площади, то если \(S_{ABC}=S\), то \(S_{ABM}=0,5S\).

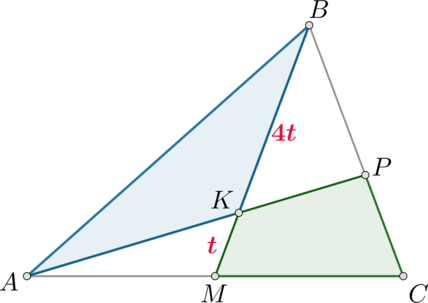
\(\triangle ABK\) и \(\triangle AMK\) имеют общую высоту, опущенную из вершины \(A\), следовательно, их площади относятся как основания (к которым проведена эта высота): \[S_{ABK}:S_{AMK}=4:1\] Значит, \(S_{ABK}=\frac45\cdot 0,5S=0,4S\), \(S_{AMK}=0,1S\).

Проведем \(ML\parallel KP\):

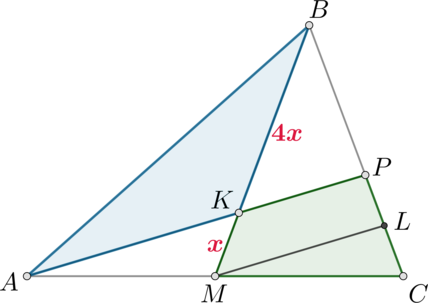
По теореме Фалеса для \(ML\parallel KP\) имеем \(MK:KB=LP:PB=1:4\). Следовательно, можно принять \(PB=4x\), \(LP=x\). По теореме Фалеса для \(AP\parallel ML\) имеем \(PL:LC=AM:MC=1:1\), следовательно, \(LC=PL=x\). Тогда \(BP:PC=4:2=2:1\). Тогда \(\triangle ABP\) и \(\triangle ACP\) также имеют общую высоту, опущенную из вершины \(A\), следовательно, \[S_{ABP}:S_{ACP}=2:1\] Отсюда \(S_{ACP}=\frac13S_{ABC}=\frac13S\). Тогда \(S_{KPCM}=\frac13S-0,1S=\frac7{30}S\). Следовательно, \[\dfrac{S_{ABK}}{S_{KPCM}}=\dfrac{0,4S}{\frac7{30}S}=\dfrac{12}7\]

Ответ: 12 : 7

Задание 2 #5231

Медиана \(BM\) и биссектриса \(AP\) треугольника \(ABC\) пересекаются в точке \(K\), длина стороны \(AC\) относится к длине стороны \(AB\) как \(9:7\). Найдите отношение площади треугольника \(ABK\) к площадь четырехугольника \(KPCM\).

Показать решение

Если \(AC:AB=9:7=18:14\), то \(AM:AB=9:14\) (\(AM\) – половина \(AC\)). Пусть \(AM=9x\), \(AB=14x\), \(S_{ABC}=S\).

Так как медиана треугольника делит его на два равновеликих, то \(S_{ABM}=\frac12S_{ABC}=\frac12S\). Так как \(AK\) – биссектриса, то \(BK:MK=AB:AM=14:9\) и \(BP:CP=AB:AC=14:18=7:9\).
Так как \(\triangle ABK\) и \(\triangle AMK\) имеют общую высоту из вершины \(A\), то \(S_{ABK}:S_{AMK}=BK:MK=14:9\). Следовательно, \(S_{ABK}=\frac{14}{14+9}S_{ABM}=\frac7{23}S\). Тогда \(S_{AMK}=\frac12S-\frac7{23}S=\frac9{46}S\).

Аналогично \(\triangle ABP\) и \(\triangle ACP\) имеют общую высоту из \(A\), следовательно, \(S_{ABP}:S_{ACP}=BP:CP=7:9\), откуда \(S_{ACP}=\frac9{16}S_{ABC}=\frac9{16}S\). Следовательно, \(S_{KPCM}=S_{ACP}-S_{AMK}=\frac{9\cdot 15}{8\cdot 46}S\). Тогда \[S_{ABK}:S_{KPCM}=\dfrac{7S}{23}:\dfrac{9\cdot 15S}{8\cdot 46}=\dfrac{112}{135}\]

Ответ: 112 : 135