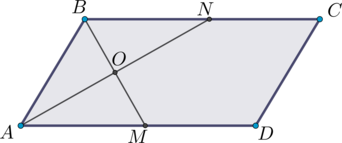
В параллелограмме \(ABCD\) на стороне \(BC\) выбрана точка \(N\) так, что \(AB = BN\), \(\angle B = 150^{\circ}\). Найдите \(\angle NAD\). Ответ дайте в градусах.
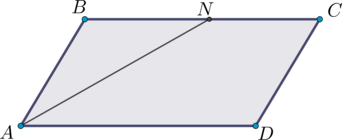
Так как в равнобедренном треугольнике углы при основании равны, то \(\angle BAN = \angle BNA\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle BAN = \angle BNA = 15^{\circ}\).
Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то \(\angle NAD = \angle BNA = 15^{\circ}\).
Ответ: 15