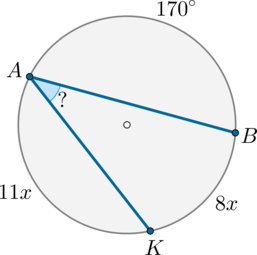
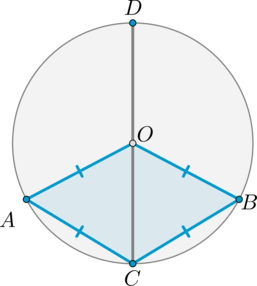
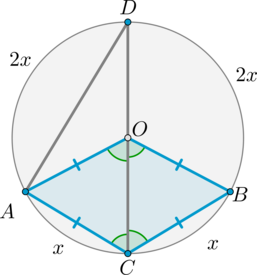
Сторона \(AB\) тупоугольного треугольника \(ABC\) равна радиусу описанной около него окружности. Найдите тупой угол \(C\). Ответ дайте в градусах.
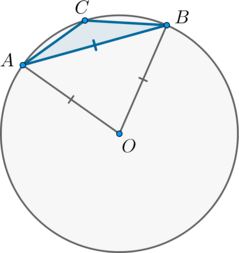
\(\triangle AOB\) равносторонний, следовательно, \(\angle
AOB=\buildrel\smile\over{AB}=60^\circ\). Тогда большая дуга \(AB\) равна \(360^\circ-60^\circ=300^\circ\). Угол \(ACB\) – вписанный угол, опирающийся на большую дугу \(AB\), следовательно, равен ее половине: \(\angle ACB=\frac12\cdot 300^\circ=150^\circ.\)
Ответ: 150