17. Окружность
Из точки \(A\) вне окружности проведена касательная \(AB\) и секущая \(AD\), как показано на картинке.
Найдите длину отрезка \(CD\), если \(AC=5\), а длина отрезка касательной равна \(10\).
Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то \[AB^2=AC\cdot AD=AC\cdot (AC+CD),\] откуда \[10^2=5\cdot (5+CD) \quad \Rightarrow \quad CD=15.\]
Ответ: 15
Из точки \(A\) вне окружности проведена касательная \(AB\) и секущая \(AD\), как показано на картинке.
Найдите длину отрезка \(AC\), если \(CD=14\), а \(AB=6\sqrt2\).
Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то \[AB^2=AC\cdot AD=AC\cdot (AC+CD),\] откуда \[(6\sqrt2)^2=AC\cdot (AC+14) \quad \Rightarrow \quad AC^2+14AC-72=0 \quad \Rightarrow \quad AC=4 \text{ или } AC=-18\]
Т.к. длина отрезка – неотрицательное число, то \(AC=4\).
Ответ: 4
Диаметр \(AA_1\) окружности пересекает хорду \(BB_1\) под прямым углом в точке \(C\), причем делится этой точкой на отрезки длиной \(18\) и \(32\), считая от точки \(A\). Найдите \(BB_1\).
Рассмотрим картинку:
Проведем из центра окружности точки \(O\) радиус \(OB\). Т.к. весь диаметр равен \(18+32=50\), то радиус равен \(25\). Следовательно, \(OB=25, \ OC=25-18=7\).
Т.к. радиус, перпендикулярный хорде, делит ее пополам, то \(BC=CB_1\). Найдем \(BC\). Треугольник \(BOC\) – прямоугольный, следовательно, \[BC^2=BO^2-OC^2 \quad \Rightarrow \quad BC^2=25^2-7^2=24^2 \quad \Rightarrow \quad BC=24\]
Значит, \(BB_1=2BC=48\).
Ответ: 48
Из некоторой точки \(C\) на окружности к диаметру \(AB\) проведен перпендикуляр \(CH\), причем \(H\) разделила диаметр на отрезки длиной \(28\) и \(7\), считая от точки \(A\). Найдите длину отрезка \(CH\).
Рассмотрим картинку:
Т.к. угол \(ACB\) опирается на диаметр, то он прямой. Следовательно, треугольник \(ABC\) прямоугольный, и \(CH\) – высота, опущенная из вершины прямого угла. Следовательно, она делит треугольник \(ABC\) на два подобных треугольника \(ACH\) и \(BCH\). Значит:
\[\dfrac{AH}{CH}=\dfrac{CH}{HB} \quad \Rightarrow \quad CH^2=AH\cdot HB \quad \Rightarrow \quad CH=\sqrt{28\cdot 7}=14.\]
Ответ: 14
Из точки \(A\) вне окружности проведены две касательные \(AB\) и \(AC\). Через произвольную точку \(X\) на окружности проведена касательная к окружности, пересекающая отрезки \(AB\) и \(AC\) в точках \(M\) и \(N\) соответственно. Найдите угол \(MON\), если \(\angle BAC=32^\circ\). Ответ дайте в градусах.
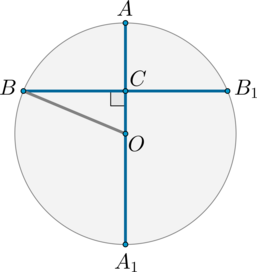
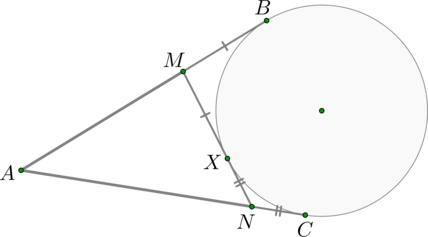
Рассмотрим картинку (пусть \(B, C\) – точки касания):
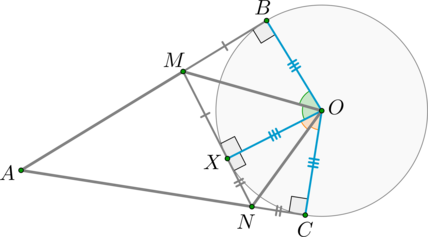
Т.к. отрезки касательных, проведенные из одной точки, равны, то \(MB=MX\) и \(NC=NX\). Т.к. радиусы, проведенные в точку касания, перпендикулярны касательной, то \(\angle OCN=\angle OXN=\angle
OXM=\angle OBM=90^\circ\). Таким образом, по двум катетам равны треугольники: \(\triangle OBM=\triangle OXM\) и \(\triangle OXN=\triangle OCN\).
Значит, \(\angle BOM=\angle XOM\) и \(\angle XON=\angle CON\).
Следовательно, \(\angle MON=\frac12 \angle BOC\).
Т.к. в четырехугольнике сумма углов равна \(360^\circ\), то в четырехугольнике \(ABOC\): \[\angle BOC=360^\circ-90^\circ-90^\circ-\angle A=180^\circ-\angle A.\]
Следовательно, \[\angle MON=\dfrac12\left(180^\circ-\angle A\right)=90^\circ-\dfrac12\angle A=90^\circ-\dfrac12\cdot 32^\circ=74^\circ.\]
Ответ: 74
Из точки \(A\) вне окружности проведены две касательные \(AB\) и \(AC\) (где \(B, C\) – точки касания). Через произвольную точку \(X\) на окружности проведена касательная к окружности, пересекающая отрезки \(AB\) и \(AC\) в точках \(M\) и \(N\) соответственно. Найдите периметр треугольника \(AMN\), если \(AB=10\).
Рассмотрим картинку:
Т.к. отрезки касательных, проведенные из одной точки, равны, то \(AB=AC=10\), \(MB=MX\) и \(NC=NX\).
Следовательно, периметр
\(P_{\triangle AMN}=AM+MN+AN=AM+(MX+XN)+AN=\)
\(=AM+(MB+NC)+AN=(AM+MB)+(NC+AN)=AB+AC=10+10=20.\)
Ответ: 20
В треугольнике \(ABC\): \(\angle C = 90^{\circ}\), \(AB = 10\), \(CO\) – медиана. Найдите длину \(CO\).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине. Покажем это:
Опишем около треугольника \(ABC\) окружность
\(\angle ACB = 90^{\circ}\) – вписанный, тогда он равен половине градусной меры дуги, на которую опирается, следовательно, градусная мера дуги \(AB\) равна \(180^{\circ}\), а значит, \(AB\) – диаметр и \(O\) – центр описанной около \(ABC\) окружности, тогда \(AO = OC\) как радиусы. \[OC = AO = 0,5 \cdot AB = 5.\]
Ответ: 5
