Отрезки \(AB\) и \(DC\) лежат на параллельных прямых, а отрезки \(AC\) и \(BD\) пересекаются в точке \(M\). Найдите \(MC\), если \(AB=14\), \(DC=42\), \(AC=52\).

Показать решение

Обозначим \(MC=x\). Тогда \(AM=52-x\). Рассмотрим чертеж:

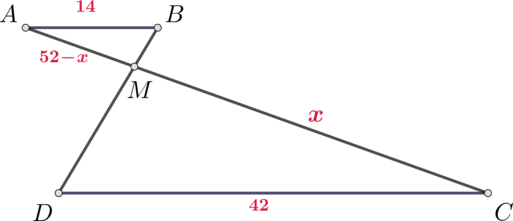
Так как \(AB\parallel CD\), то накрест лежащие углы при параллельных прямых и секущей \(BD\) равны, то есть \(\angle ABM=\angle CDM\). Также \(\angle AMB=\angle CMD\) как вертикальные. Следовательно, \(\triangle ABM\sim \triangle CMD\) по двум углам. Отсюда получаем: \[\dfrac{AB}{CD}=\dfrac{AM}{MC}\quad \Rightarrow\quad \dfrac{14}{42}=\dfrac{52-x}x\quad \Rightarrow\quad x=39.\]

Ответ: 39

Задание 2 #5173

Прямая, параллельная стороне \(AC\) треугольника \(ABC\), пересекает стороны \(AB\) и \(BC\) в точках \(K\) и \(M\) соответственно. Найдите \(AC\), если \(BK:KA=3:4\), \(KM=18\).

Показать решение

Так как \(BK:KA=3:4\), то можно обозначить \(BK=3x\), \(KA=4x\). Рассмотрим чертеж:

Так как \(KM\parallel AC\), то \(\angle BKM=\angle BAC\) как соответственные при секущей \(AB\). Также \(\angle B\) – общий для \(\triangle ABC\) и \(\triangle KBM\). Следовательно, по двум углам \(\triangle ABC\sim \triangle KBM\). Тогда можно записать \[\dfrac{KM}{AC}=\dfrac{KB}{BA}\quad \Rightarrow\quad \dfrac{18}{AC}=\dfrac{3x}{7x}\quad\Rightarrow\quad AC=42.\]

Ответ: 42

Задание 3 #5174

Прямая, параллельная стороне \(AC\) треугольника \(ABC\), пересекает стороны \(AB\) и \(BC\) в точках \(M\) и \(N\) соответственно. Найдите \(BN\), если \(MN=17\), \(AC=51\), \(NC=32\).

Показать решение

Обозначим \(BN=x\). Рассмотрим чертеж:

Так как \(NM\parallel AC\), то \(\angle BMN=\angle BAC\) как соответственные при секущей \(AB\). Также \(\angle B\) – общий для \(\triangle ABC\) и \(\triangle MBN\). Следовательно, по двум углам \(\triangle ABC\sim \triangle MBN\). Тогда можно записать \[\dfrac{BN}{BC}=\dfrac{MN}{AC}\quad \Rightarrow\quad \dfrac{x}{x+32}=\dfrac{17}{51}\quad\Rightarrow\quad x=16.\]

Ответ: 16

Задание 4 #5175

Катеты прямоугольного треугольника равны \(18\) и \(24\). Найдите высоту, проведенную к гипотенузе.

Показать решение

Рассмотрим прямоугольный \(\triangle ABC\) и его высоту \(CH=h\):

С одной стороны, площадь прямоугольного треугольника равна \(S=\frac12 AC\cdot BC\). С другой стороны, \(S=\frac12 CH\cdot AB\).
Найдем \(AB\) по теореме Пифагора: \(AB=\sqrt{18^2+24^2}=30\).
(Легкий способ вычисления: заметим, что прямоугольный треугольник с катетами 18 и 24 подобен прямоугольному треугольнику с катетами 3 и 4 с коэффициентом подобия 6. Следовательно, если у треугольника с катетами 3 и 4 гипотенуза равна 5, то у треугольника с катетами 18 и 24 гипотенуза равна \(5\cdot 6=30\).)

Таким образом, получаем: \[\dfrac12\cdot 18\cdot 24=\dfrac 12\cdot h\cdot 30\quad\Rightarrow\quad h=14,4\]

Ответ: 14,4

Задание 5 #5176

Точка \(H\) является основанием высоты, проведенной из вершины прямого угла \(B\) треугольника \(ABC\) к гипотенузе \(AC\). Найдите \(AB\), если \(AH=6\), \(AC=24\).

Показать решение

Из условия следует, что \(CH=24-6=18\). Рассмотрим чертеж:

По свойству прямоугольного треугольника высота, проведенная из вершины прямого угла, есть среднее геометрическое между отрезками, на которые она делит гипотенузу, то есть \(BH=\sqrt{AH\cdot HC}\). Следовательно, \(BH=\sqrt{6\cdot 18}=6\sqrt3\).
Тогда по теореме Пифагора для \(\triangle AHB\): \[AB=\sqrt{(6\sqrt3)^2+6^2}=12.\]

Ответ: 12