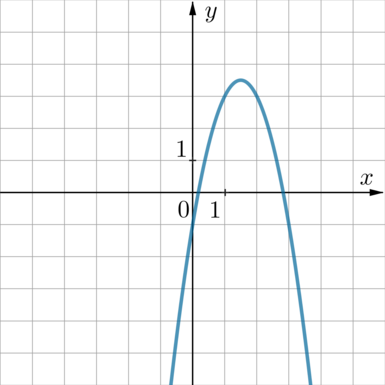
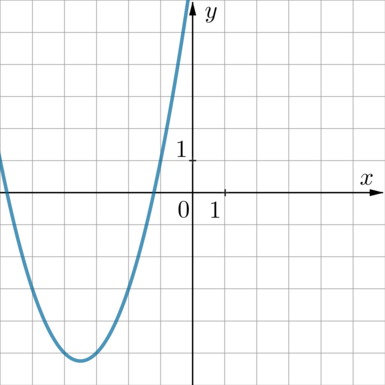
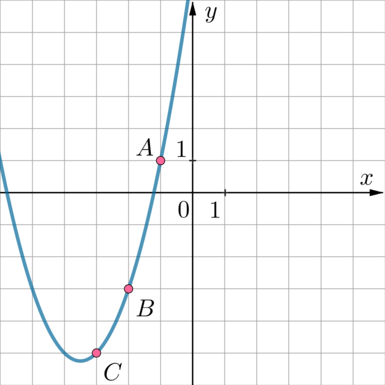
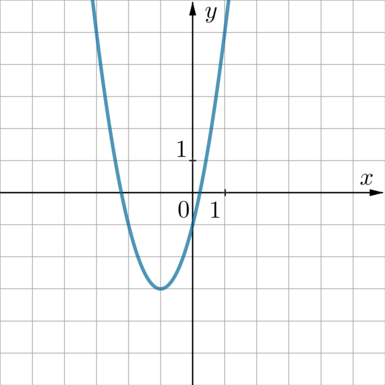
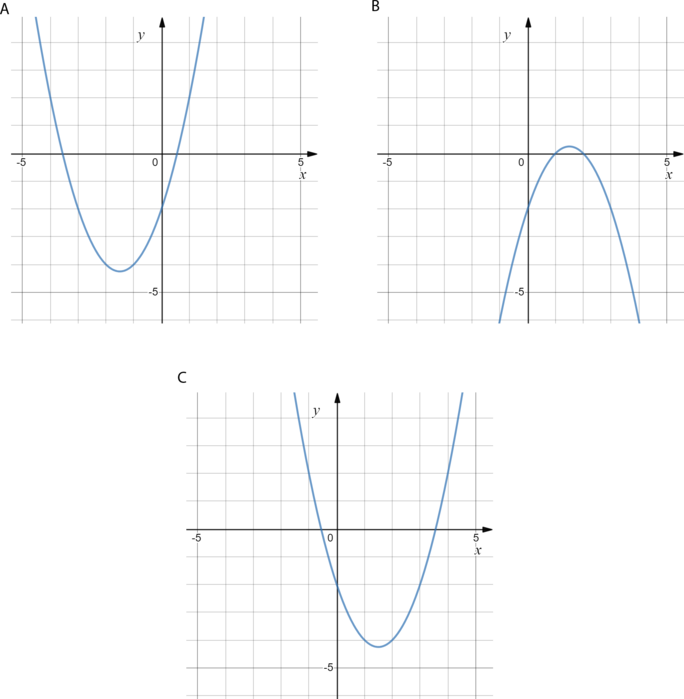
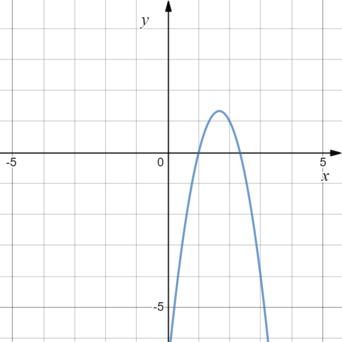
График какой из приведенных ниже функций изображен на рисунке?
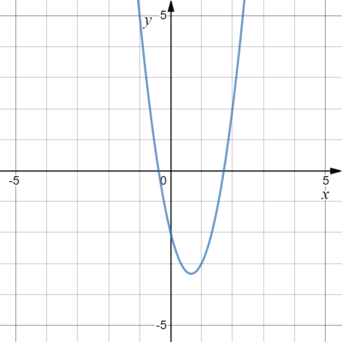
1) \(y=-3x^2-4x+2\) \(\;\;\;\) 2)\(y=-3x^2-4x-2\) \(\;\;\;\) 3)\(y=3x^2-4x+2\) \(\;\;\;\) 4)\(y=3x^2-4x-2\)
Общее уравнение параболы имеет вид \(y=ax^2+bx+c\), где знак \(a\) зависит от направления ветвей параболы, \(c\) — точка пересечения графика с осью \(y\).
У данной функции \(a>0\) — ветви направленны вверх, поэтому варианты 1) и 2) точно не подходят.
Так как график пересекает ось \(y\) ниже нуля, то \(c<0\). Подходит вариант 4).
Ответ: 4