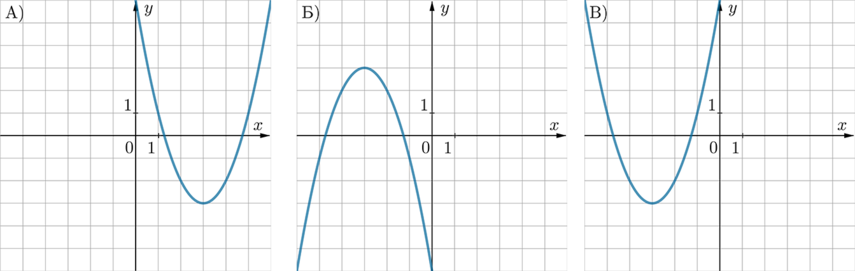
Установите соответствие между графиками функций и формулами, которые их задают.
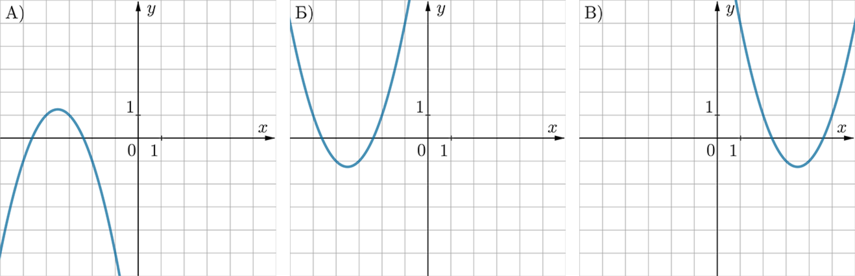
ФОРМУЛЫ:
1) \(y=-x^2-7x-11\qquad \) 2) \(y=x^2+7x+11\qquad \) 3) \(y=x^2-7x+11\)
В таблице под каждой буквой укажите соответствующий номер.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline && \\ \hline \end{array}\)
Если ветви параболы направлены вверх – то коэффициент перед \(\,x^2\) положительный, вниз – отрицательный. Парабола А – единственная, ветви которой направлены вниз, следовательно, ей соответствует формула 1.
У параболы Б абсцисса вершины отрицательная, у параболы В – положительная. Так как из формулы \(y=ax^2+bx+c\) абсцисса вершины ищется как \(x_0=\frac{-b}{2a}\), то Б – 2, В – 3.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline 1&2&3 \\ \hline \end{array}\)
В ответ запишем 123.
Ответ: 123