17. Окружность
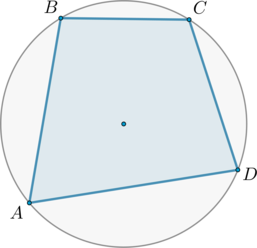
Четырехугольник \(ABCD\) вписан в окружность. Угол \(ABC\) равен \(110^\circ\), угол \(ABD\) равен \(70^\circ\). Найдите угол \(CAD\). Ответ дайте в градусах.
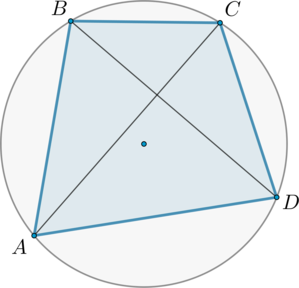
Вписанные углы, опирающиеся на равные дуги, равны. Следовательно, \(\angle CAD=\angle CBD\).
\(\angle CBD=\angle ABC-\angle ABD=110^\circ-70^\circ=40^\circ\).
Ответ: 40
Сторона \(AB\) треугольника \(ABC\) равна \(1\). Противолежащий ей угол \(C\) равен \(150^\circ\). Найдите радиус окружности, описанной около этого треугольника.
По теореме синусов \[\dfrac{AB}{\sin\angle C}=2R\] Следовательно, \[R=\dfrac12\cdot \dfrac{1}{\sin150^\circ}=\dfrac12\cdot \dfrac1{\frac12}=1\]
Ответ: 1
Угол \(C\) треугольника \(ABC\), вписанного в окружность радиуса \(3\), равен \(30^\circ\). Найдите сторону \(AB\) этого треугольника.
По теореме синусов \[\dfrac{AB}{\sin\angle C}=2R\] Следовательно, \[AB=2R\cdot \sin\angle C=2\cdot 3\cdot \sin30^\circ=3\]
Ответ: 3
Одна сторона остроугольного треугольника равна радиусу описанной около него окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
Пусть \(AB=R\). Тогда нужно найти \(\angle C\). По теореме синусов: \[\dfrac{AB}{\sin \angle C}=2R\quad\Rightarrow\quad \sin\angle C=\dfrac{AB}{2R}=\dfrac R{2R}=\dfrac12\] Так как треугольник остроугольный, то \(\angle C=30^\circ\).
Ответ: 30
Сторона \(AB\) треугольника \(ABC\) равна \(1\). Противолежащий ей угол \(C\) равен \(30^\circ\). Найдите радиус окружности, описанной около этого треугольника.
По теореме синусов \[\dfrac{AB}{\sin\angle C}=2R\] Следовательно, \[R=\dfrac12\cdot \dfrac{1}{\sin30^\circ}=\dfrac12\cdot \dfrac1{\frac12}=1\]
Ответ: 1
Стороны \(AB, BC, CD, AD\) четырехугольника \(ABCD\) стягивают дуги описанной окружности, градусные меры которых равны соответственно \(95^\circ, 49^\circ, 71^\circ, 145^\circ\). Найдите угол \(B\) этого четырехугольника. Ответ дайте в градусах.
Угол \(B\) четырехугольника равен вписанному углу \(ABC\). Этот угол опирается на дугу \(\buildrel\smile\over{ADC}\), равную \(145^\circ+71^\circ=216^\circ\). Так как вписанный угол равен половине дуги, на которую он опирается, то \(\angle B=\angle ABC=108^\circ\).
Ответ: 108
Угол \(A\) четырехугольника \(ABCD\), вписанного в окружность, равен \(58^\circ\). Найдите угол \(C\) этого четырехугольника. Ответ дайте в градусах.
Так как четырехугольник вписан в окружность, то сумма противоположных его углов равна \(180^\circ\). Следовательно, \(\angle A+\angle C=180^\circ\), откуда \(\angle C=180^\circ-58^\circ=122^\circ\).
Ответ: 122
