19. Задачи на клетчатой бумаге
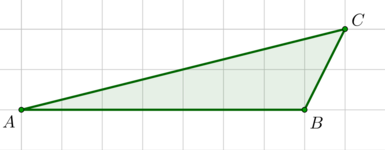
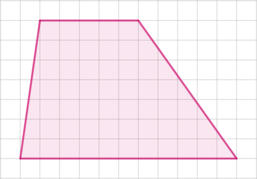
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки \(1\) см \(\times\) \(1\) см. Ответ дайте в квадратных сантиметрах.
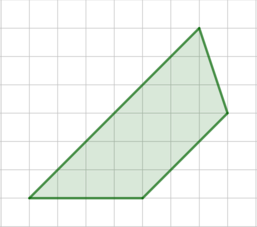
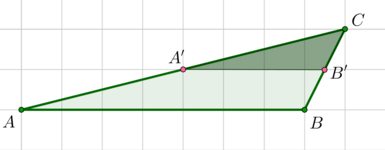
Опишем вокруг трапеции прямоугольник, как показано на рисунке:
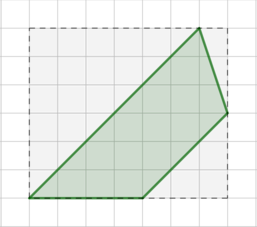
Тогда для того, чтобы найти площадь трапеции, нужно из площади этого прямоугольника вычесть площади трех прямоугольных треугольников: \[S=6\cdot 7-\left(\dfrac12\cdot 6\cdot 6+\dfrac12\cdot 1\cdot 3+\dfrac12
\cdot 3\cdot 3\right)=18\]
Ответ: 18
На клетчатой бумаге с размером клетки \(1\times 1\) изображен треугольник \(ABC\). Найдите площадь треугольника \(A'B'C\), где \(A'B'\) – средняя линия, параллельная стороне \(AB\).
Пусть \(A'\in AC, B'\in BC\).
По свойству средней линии \(\triangle ABC\sim \triangle A'B'C\) с коэффициентом подобия, равным \(2\). Следовательно, их площади относятся как коэффициент подобия в квадрате, то есть \[\dfrac{S_{ABC}}{S_{A'B'C}}=4\] Высота \(\triangle ABC\), опущенная из \(C\), равна \(2\), \(AB=7\). Следовательно, \(S_{ABC}=\frac12\cdot 2\cdot 7=7\). Тогда \[S_{A'B'C}=\dfrac74=1,75.\]
Ответ: 1,75
На клетчатой бумаге с размером клетки \(1\times 1\) изображен треугольник \(ABC\). Найдите длину средней линии, параллельной стороне \(AB\).
Длина средней линии треугольника, параллельной стороне \(AB\), равна \(\frac12AB\). Так как \(AB=7\), то средняя линия равна \(3,5\).
Ответ: 3,5
На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна \(3\).
Будем искать радиус вписанной окружности по формуле \(S=p\cdot r\), где \(S\) – площадь, \(p\) – полупериметр.
Заметим, что треугольник равнобедренный: \(AB=BC.\)
Так как длина стороны клетки равна \(3\), то \(AH=12, BH=9\), следовательно, \(AB=\sqrt{AH^2+BH^2}=15.\) Тогда \[\dfrac12\cdot BH\cdot AC=\dfrac{AB+BC+AC}2\cdot r \quad\Rightarrow\quad
r=4.\]
Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна \(1\), а затем умножать полученный ответ на \(3\). Если бы длина одной клетки была равна \(1\), то \(AH=4, BH=3\), \(AB=5\) и \(r=\frac43\). Тогда после умножения на \(3\) также получили бы \(r=4\). При решении задачи таким способом вычисления будут легче.
Ответ: 4
На клетчатой бумаге с размером клетки \(1\times1\) изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме оснований. Большее основание равно \(11\), меньшее равно \(5\), следовательно, средняя линия равна \((11+5):2=8\).
Ответ: 8
На клетчатой бумаге с размером клетки \(1\times1\) изображен ромб. Найдите его площадь.
Проведем диагонали данного ромба:
Площадь ромба равна полупроизведению диагоналей, следовательно, \[S=\dfrac12\cdot 4\cdot 6=12\]
Ответ: 12
На клетчатой бумаге изображен угол. Найдите его градусную величину.
Обозначим этот угол \(ASD\). Отметим точку \(F\) так, чтобы получился прямоугольный \(\triangle SDF\):
Тогда \(\angle ASD=\angle ASF+\angle FSD\). Заметим, что \(\angle
ASF=90^\circ\). Заметим также, что \(FS=FD\), следовательно, \(\triangle
SDF\) прямоугольный и равнобедренный, значит, его острые углы равны по \(45^\circ\).
Следовательно, \[\angle ASD=90^\circ+45^\circ=135^\circ.\]
Ответ: 135
