В треугольнике \(ABC\): \(\angle A = 32^{\circ}\), \(\angle B =
70^{\circ}\). На продолжении стороны \(AC\) за точку \(C\) отложен отрезок \(CK = BC\). Найдите \(\angle K\) треугольника \(BCK\). Ответ дайте в градусах.
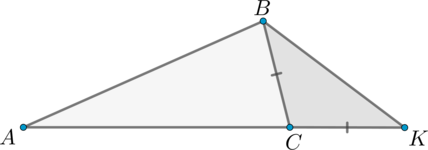
У равнобедренного треугольника углы при основании равны. Так как \(CK = BC\), то \(\angle CBK = \angle K\).
Согласно теореме о внешнем угле треугольника, \(\angle BCK = \angle A + \angle ABC = 32^{\circ} + 70^{\circ} = 102^{\circ}\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle BCK + \angle CBK + \angle K = 180^{\circ}\), но \(\angle CBK = \angle K\), тогда \(102^{\circ} + 2\cdot \angle K = 180^{\circ}\), откуда находим \(\angle K = 39^{\circ}\).
Ответ: 39