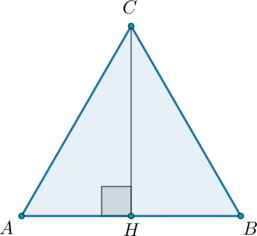
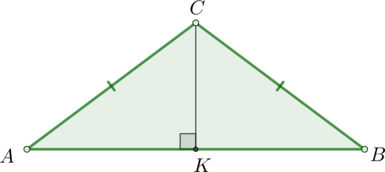
В треугольнике \(ABC\) \(AC=BC=2\sqrt3\), \(\angle C=120^\circ\). Найдите высоту \(AH\).
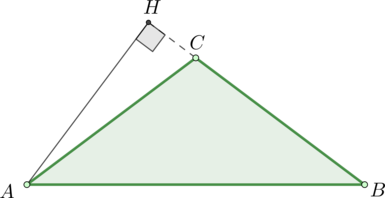
Рассмотрим прямоугольный \(\triangle ACH\). Так как \(\angle ACB=120^\circ\), то \(\angle ACH=180^\circ-120^\circ=60^\circ\). Следовательно, \(\angle HAC=90^\circ-60^\circ=30^\circ\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(HC=0,5AC=\sqrt3\). Тогда по теореме Пифагора \[AH=\sqrt{AC^2-HC^2}=3\]
Ответ: 3