Работа с окружностью

Если из центра окружности к хорде провести перпендикуляр, то он разделит хорду пополам.
(Действительно, рассмотрим хорду \(AB\). Проведем радиусы \(AO\) и \(BO\). Тогда \(\triangle AOB\) равнобедренный и \(OH\) – высота равнобедренного треугольника, проведенная к основанию. Следовательно, она является и медианой, то есть \(AH=HB\). Чтд.)



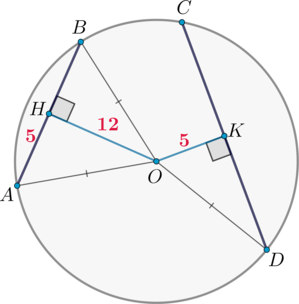
Аналогично \(CK=KD\).

Рассмотрим прямоугольный \(\triangle AHO\). По теореме Пифагора \(AO=\sqrt{5^2+12^2}=13\). Следовательно, \(DO=AO=13\). Тогда из прямоугольного \(\triangle OKD\): \(KD=\sqrt{13^2-5^2}=12\). Тогда \(CD=24\).

(Можно было также заметить, что \(\triangle AHO=\triangle OKD\) как прямоугольные по катету и гипотенузе. Следовательно, \(HO=KD\).)

Ответ: 24

Способ 1.

Если в четырехугольник вписана окружность, то суммы противоположных сторон четырехугольника равны. Следовательно, если \(ABCD\) – параллелограмм, в который вписана окружность, и \(AB=5\) по условию, то \(AB+CD=AD+BC=10\) (\(AB=CD=5\) как противоположные стороны параллелограмма). Следовательно, периметр параллелограмма равен \(10+10=20\).

Способ 2. Не используя факт из способа 1.

Пусть дан параллелограмм \(ABCD\), \(O\) – центр окружности. Проведем \(OA\), \(OC\), \(OD\). Так как центр вписанной окружности лежит на пересечении биссектрис углов многоугольника, то \(OA\), \(OC\), \(OD\) – биссектрисы углов \(A\), \(C\), \(D\) параллелограмма.
Биссектрисы односторонних углов при двух параллельных прямых перпендикулярны, следовательно, \(\angle AOD=90^\circ\).
(Действительно, так как \(AB\parallel CD\), то односторонние углы \(\angle BAD\) и \(\angle ADC\) в сумме дают \(180^\circ\) (при секущей \(AD\)). Так как \(AO\), \(DO\) – биссектрисы, то \(\angle OAD+\angle ODA=0,5(\angle BAD+\angle ADC)=0,5\cdot 180^\circ=90^\circ\).)



Аналогично доказывается, что \(\angle COD=90^\circ\). Следовательно, \(\angle AOC=180^\circ\), то есть точки \(A, O, C\) лежат на одной прямой. Отсюда следует, что \(AC\) – и диагональ параллелограмма, и биссектриса его углов.
Аналогично доказывается, что \(BD\) – диагональ и биссектриса углов параллелограмма.
Если диагонали параллелограмма являются биссектрисами его углов, то этот параллелограмм является ромбом. Следовательно, все стороны ромба \(ABCD\) равны по \(5\), то есть его периметр равен \(20\).

(В данной задаче мы доказали, что если в параллелограмм вписана окружность, то он является ромбом. Данный факт можно запомнить.)

Ответ: 20

Рассмотрим трапецию \(ABCD\), \(AB+CD=16\). Средняя линия трапеции равна полусумме ее оснований, следовательно, нужно найти \(0,5(AD+BC)\).



Если в четырехугольник вписана окружность, то суммы его противоположных сторон равны, следовательно, \(AB+CD=AD+BC\). Следовательно, средняя линия трапеции равна \(0,5\cdot 16=8\).

Ответ: 8

Так как \(\angle B=71^\circ\), \(\angle C=79^\circ\), то \(\angle A=180^\circ-71^\circ-79^\circ=30^\circ\).



По теореме синусов \[\dfrac{BC}{\sin\angle A}=2R\quad\Rightarrow\quad BC=2\cdot 8\cdot \dfrac12=8.\]

Ответ: 8

Так как в задаче нужно найти радиус описанной около треугольника окружности и дана сторона треугольника, то будем пользоваться теоремой синусов: \(\frac a{\sin \alpha}=2R\). Следовательно, найдем угол, лежащий против стороны, равной \(12\).
Так как дуги делятся в отношении \(6:7:23\), то примем \(\buildrel\smile\over{AB}=6x\), \(\buildrel\smile\over{BC}=7x\), \(\buildrel\smile\over{CA}=23x\) (см. рисунок):



Так как вся окружность составляет \(360^\circ\), то \(6x+7x+23x=360^\circ\), откуда \(x=10^\circ\).
Тогда \(\buildrel\smile\over{AB}=60^\circ\), следовательно, \(\angle C=30^\circ\) как вписанный угол, опирающийся на эту дугу. Заметим также, что это меньший угол треугольника (так как \(\angle ABC\) и \(\angle BAC\) вписанные и опираются на дуги, большие, чем дуга, на которую опирается \(\angle BCA\)).
Так как в треугольника против меньшего угла лежит меньшая сторона, то \(AB=12\).
Следовательно, по теореме синусов: \[\dfrac{AB}{\sin\angle C}=2R\quad\Rightarrow\quad R=\dfrac{12}{\frac12}:2=12.\]

Ответ: 12

Рассмотрим рисунок:



Вспомним факты, связанные со вписанной и описанной окружностями и с углами: 1) центр вписанной окружности лежит на пересечении биссектрис; 2) вписанные и центральные углы; 3) стороны треугольника \(ABC\) являются касательными к окружности.
Воспользуемся фактом 2: вписанный угол равен половине дуги, на которую он опирается. Так как \(\angle MKP\) является вписанным углом, то \(\buildrel\smile\over{MP}=2\cdot 56^\circ=112^\circ\). Аналогично \(\buildrel\smile\over{MK}=114^\circ\), \(\buildrel\smile\over{KP}=134^\circ\).
Воспользуемся фактом 3: \(CK\) и \(CP\) – касательные к окружности, проведенные из одной точки. Следовательно, угол между ними равен полуразности дуг, заключенных между ними. Значит, \(\angle C=\buildrel\smile\over{KMP}-\buildrel\smile\over{KP}=0,5\left((112^\circ+114^\circ)- 134^\circ\right)=46^\circ\).
Аналогично находим, что \(\angle A=66^\circ\), \(\angle B=68^\circ\).

Ответ: 46∘, 66∘, 68∘

В данной задаче есть прямые углы и окружность, следовательно, вспоминаем факты, связывающие эти понятия. Факт 1: если вписанный угол равен \(90^\circ\), то он опирается на диаметр. В нашем случае \(\angle PBK=90^\circ\) – вписанный, следовательно, \(PK\) – диаметр окружности.
Так как по условию \(BH\) также является диаметром окружности, то \(PK=BH=14\).

Ответ: 14