18. Площади геометрических фигур
На клетчатой бумаге нарисован круг площадью \(2,8\). Найдите площадь закрашенного сектора.
Заметим, что закрашенная фигура состоит из двух непересекающихся частей, равных \(\frac14\) и \(\frac12\) от \(\frac14\) круга:
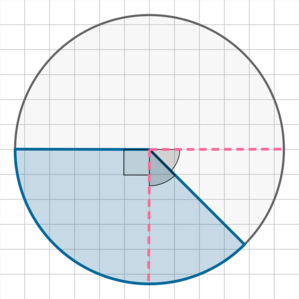
Таким образом, ее площадь равна \[\dfrac14S+\dfrac12\cdot \left(\dfrac14S\right)=\dfrac38S=\dfrac38\cdot 2,8=1,05.\]
Ответ: 1,05
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны \(\dfrac 4{\sqrt{\pi}}\) и \(\dfrac
2{\sqrt{\pi}}\).
Для того, чтобы найти площадь кольца, нужно из площади большего круга вычесть площадь меньшего круга: \[S=\pi\cdot \left(\dfrac 4{\sqrt{\pi}}\right)^2- \pi\cdot \left(\dfrac 2{\sqrt{\pi}}\right)^2= \pi\cdot \left( \dfrac{16}{\pi}-\dfrac4{\pi}\right)=12\]
Ответ: 12
Длина окружности с центром в точке \(O\) равна 12. \(\angle AOB = 120^{\circ}\), точки \(A\) и \(B\) лежат на окружности и разбивают её на две дуги. Во сколько раз длина большей из получившихся дуг превосходит длину меньшей?
Длины дуг относятся так же, как их градусные меры. Так как \(O\) – центр окружности, то \(\angle AOB\) – центральный.
Градусная мера дуги, меньшей, чем полуокружность, есть градусная мера центрального угла, который на неё опирается. Тогда градусная мера меньшей из дуг равна \(120^{\circ}\), а большей из дуг \(240^{\circ}\).
Градусная мера большей дуги в \(240 : 120 = 2\) раза больше, чем градусная мера меньшей дуги.
Ответ: 2
Длина окружности с центром в точке \(O\) равна 18 см. Площадь сектора \(AOB\) равна \(\dfrac{18}{\pi}\) см\(^2\). Найдите длину дуги \(AB\) этого сектора. Ответ дайте в сантиметрах.
Длина окружности равна \(2\pi R\), где \(R\) – радиус этой окружности. Для данной окружности \(2\pi R = 18\) см, тогда \(R = \dfrac{9}{\pi}\) см.
Площадь сектора, градусная мера дуги которого есть \(\alpha\) равна \(\pi R^2 \cdot \dfrac{\alpha}{360}\). Длина дуги с градусной мерой \(\alpha\) равна \(2\pi R\cdot \dfrac{\alpha}{360}\). Из этих формул видно, что длина дуги с градусной мерой \(\alpha\) получится из площади сектора, градусная мера дуги которого есть \(\alpha\), при помощи умножения этой площади на \(\dfrac{2}{R}\).
Длина дуги \(AB\) данного сектора равна \(\dfrac{18}{\pi} \cdot \dfrac{2\pi}{9} = 4\) см.
Ответ: 4
Внутри большой окружности расположена маленькая, радиус которой в 2,5 раза меньше, чем радиус большой окружности. Найдите отношение площади зеленой области \(U\) к площади круга, ограниченного большой окружностью.
Обозначим радиус меньшей из окружностей за \(r\), тогда радиус большей окружности \(2,5\cdot r\).
Площадь круга, ограниченного окружностью радиуса \(R\), равна \(\pi R^2\).
Площадь меньшего круга равна \(\pi r^2\), а площадь большего равна \(\pi
\cdot (2,5r)^2 = 6,25\pi r^2\).
Площадь области \(U\) равна разности площадей большего и меньшего кругов и равна \(6,25\pi r^2 - \pi r^2 = 5,25\pi r^2\).
Искомое отношение площадей есть \(\dfrac{5,25\pi r^2}{6,25\pi r^2} =
0,84\).
Ответ: 0,84
