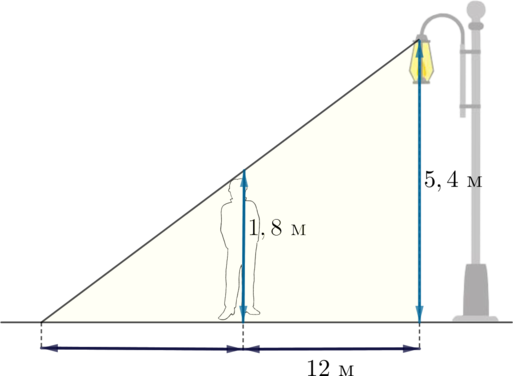
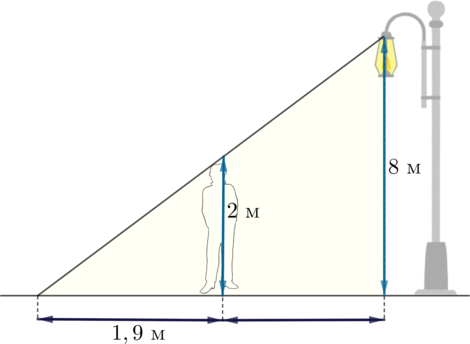
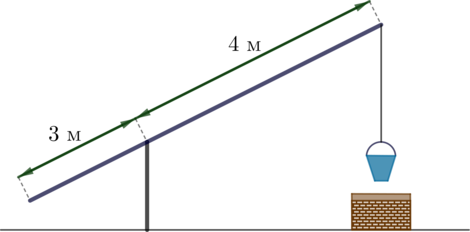
На рисунке изображен колодец с “журавлем”. Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого плеча поднимется на 1 м?
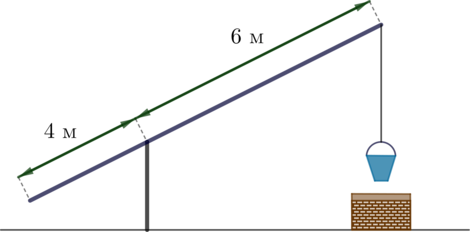
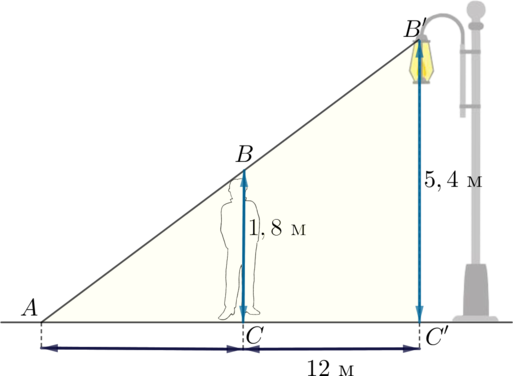
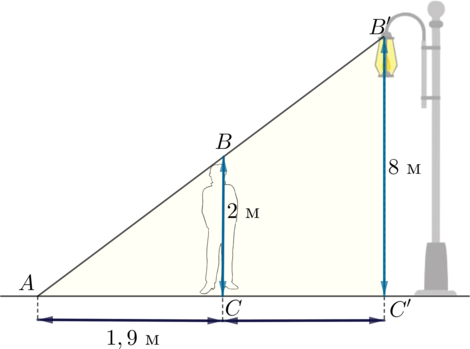
Рассмотрим чертеж колодца с “журавлем”, когда конец короткого плеча поднимется на 1 м:

Обозначим концы “журавля” в начальном положении за \(A\) и \(B\), в конечном – за \(A'\) и \(B'\). Мы получаем подобные равнобедренные треугольники \(OAA'\) и \(OBB'\). Следовательно, \[\dfrac{AA'}{BB'}=\dfrac{OA}{OB}\quad\Rightarrow\quad BB'=1,5\] (так как \(AA'=1\) по условию).
Ответ: 1,5