Площадь параллелограмма, ромба, прямоугольника и квадрата

Рассмотрим трапецию \(ABCD\), где \(AB=12, CD=12\sqrt5\), \(\angle A=45^\circ, \angle B=135^\circ\), и проведем в ней высоты \(BH\) и \(CK\). При этом трапеция может выглядеть двумя разными способами.

1 способ.

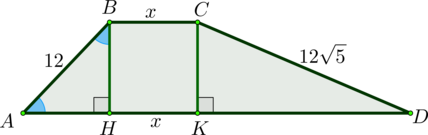
Заметим, что \(\triangle ABH\) – прямоугольный и равнобедренный, тогда \[BH=AH=\dfrac{AB}{\sqrt2}=\dfrac{12}{\sqrt2}=6\sqrt2\]

Значит, из прямоугольного \(\triangle DCK\) можно найти \(KD\):

\[KD^2=CD^2-CK^2=(12\sqrt5)^2-(6\sqrt2)^2=648 \quad \Rightarrow \quad KD=\sqrt{9\cdot 9\cdot 4 \cdot 2}=18\sqrt2\]

Т.к. площадь трапеции равна \(156\), то имеем следующее уравнение:

\[\dfrac{6\sqrt2+18\sqrt2+x+x}2\cdot 6\sqrt2=156 \quad \Rightarrow \quad x=\sqrt2\]

Тогда \(BC:AD=(\sqrt2):(25\sqrt2)=1:25\).

2 способ.

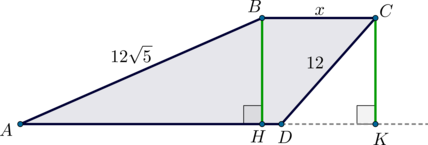
В этом случае, поступая аналогично первому способу, находим \(CK=DK=BH=6\sqrt2\), \(AH=18\sqrt2\), \(AD=18\sqrt2+x-6\sqrt2=12\sqrt2+x\).

Из уравнения \(156=\dfrac{12\sqrt2+x+x}2\cdot 6\sqrt2\) находим \(x=7\sqrt2\).

Значит, \(BC:AD=(7\sqrt2):(19\sqrt2)=7:19\).

Т.к. \(\frac1{25}<\frac7{19}\), то в ответ пойдет \(\frac1{25}=0,04\).

Ответ: 0,04

Площадь треугольника равна половине произведения основания на высоту, тогда площадь треугольника \(AED\) равна \(0,5 \cdot AD \cdot h\), где \(h\) – высота, опущенная из точки \(E\) на \(AD\). Пусть эта высота пересекает \(AD\) в точке \(F\), тогда \(FECD\) – параллелограмм (\(EF \parallel CD, \ EC \parallel FD\)), значит, \(h = CD\) и площадь прямоугольника \(ABCD\) равна \(AD \cdot h\), то есть она в два раза больше, чем площадь треугольника \(AED\) и, следовательно, равна 6.

Ответ: 6

\(AD = CD\); по теореме Пифагора находим: \(AC^2 = AD^2 + CD^2 = 2\cdot AD^2\), тогда \(AD^2 = 50\), но площадь квадрата \(ABCD\) и равна \(AD^2\).

Ответ: 50

Пусть \(E\) – точка пересечения диагоналей квадрата \(ABCD\).

В квадрате диагонали равны и точкой пересечения делятся пополам, тогда \(AE = ED \ \Rightarrow \triangle ADE \) — равнобедренный.

Опустим из точки \(E\) высоту \(EF\) на \(AD\) (длина \(EF\) и есть расстояние от точки \(E\) до стороны). Так как \(\triangle ADE \) — равнобедренный, то \(EF\) является и медианой, но в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(EF = 0,5\cdot AD\).

Тогда \(AD = 10\), следовательно, площадь квадрата \(ABCD\) равна \(100\).

Ответ: 100

Площадь прямоугольника равна \(S_1=ab\), площадь параллелограмма равна \(S_2=ab\cdot \sin\alpha\). Из условия следует, что \(2S_2=S_1\). Следовательно: \[2ab\cdot \sin\alpha=ab\quad\Rightarrow\quad \sin\alpha=\dfrac12\quad\Rightarrow \quad \alpha=30^\circ\]

Ответ: 30

В параллелограмме противоположные углы равны, а односторонние углы в сумме составляют \(180^{\circ}\).

Так как \(\sin{(\pi - \alpha)} = \sin{\alpha}\), то \(\sin{\angle A} + \sin{\angle B} + \sin{\angle C} + \sin{\angle D} = 4 \sin{\angle A}\), откуда находим \(\sin{\angle A} = 0,81\).

Площадь параллелограмма равна произведению двух его непараллельных сторон на синус угла между ними, тогда \[S_{ABCD} = 6\cdot 5\cdot 0,81 = 24,3.\]

Ответ: 24,3

В ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, тогда \(OD = 4\), \(\dfrac{CO}{OD} = \mathrm{tg}\, \angle BDC = 3\), откуда \(CO = 12\), следовательно, \(AC = 24\).

Площадь ромба равна половине произведения его диагоналей, тогда \[S_{ABCD} = 0,5\cdot 8\cdot 24 = 96.\]

Ответ: 96