Прямая, параллельная основаниям трапеции $ABCD$, пересекает ее боковые стороны $AB$ и $CD$ в точках $E$ и $F$ соответственно. Найдите длину отрезка $EF$, если $AD=42$, $BC=14$, $CF:DF=4:3$.

Показать решение

Проведем $AC$. Пусть $AC$ пересекает $EF$ в точке $K$.

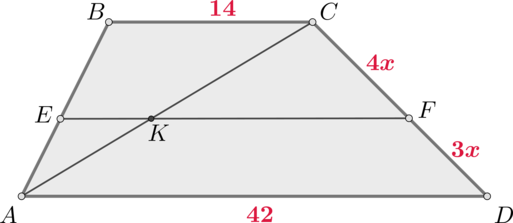
Рассмотрим $\triangle ACD$ и $\triangle KCF$. Они подобны по двум углам ($\angle C$ – общий, $\angle CFK=\angle CDA$ как соответственные при $KF\parallel AD$ и секущей $CD$). Следовательно, \[\dfrac{CF}{CD}=\dfrac{KF}{AD}\quad\Rightarrow\quad \dfrac47=\dfrac{KF}{42} \quad\Rightarrow\quad KF=24.\]

Так как $EF\parallel AD\parallel BC$, то по теореме Фалеса $BE:EA=CF:FD=4:3$.

Аналогично доказывается, что $\triangle BAC\sim \triangle EAK$, следовательно, \[\dfrac{AE}{AB}=\dfrac{EK}{BC}\quad\Rightarrow\quad \dfrac37=\dfrac{EK}{14} \quad\Rightarrow\quad EK=6.\]

Отсюда находим, что $EF=24+6=30.$

Ответ: 30

Задание 2 #5143

Найдите боковую сторону $AB$ трапеции $ABCD$, если углы $ABC$ и $BCD$ равны соответственно $60^\circ$ и $135^\circ$, а $CD=36$.

Показать решение

Проведем $BK\perp AD$, $CH\perp AD$ – высоты.

Так как в трапеции сумма углов при боковой стороне равна $180^\circ$, то $\angle ADC=45^\circ$. Следовательно, прямоугольный $\triangle CHD$ является равнобедренным, откуда следует, что $CH=HD$. Тогда по теореме Пифагора из этого треугольника: $36^2=CH^2+CH^2$, откуда $CH=18\sqrt2$.
Так как высоты трапеции равны, то $BK=CH=18\sqrt2$.
Рассмотрим прямоугольный $\triangle ABK$. Угол $KBC=90^\circ$, следовательно, $\angle KBA=30^\circ$. Так как катет, лежащий против угла $30^\circ$, равен половине гипотенузы, то $AB=2KA$. Обозначим $KA=x$, $AB=2x$. Тогда по теореме Пифагора из этого треугольника \[(2x)^2=x^2+(18\sqrt2)^2\quad\Rightarrow\quad x=6\sqrt6\quad\Rightarrow\quad 2x=12\sqrt6\]

Ответ: $12\sqrt6$

Задание 3 #5144

Биссектриса угла $A$ параллелограмма $ABCD$ пересекает сторону $BC$ в точке $K$. Найдите периметр параллелограмма, если $BK=7$, $CK=12$.

Показать решение

По свойству параллелограмма биссектриса, проведенная из его угла, отсекает от него равнобедренный треугольник, то есть $\triangle ABK$ – равнобедренный ($AB=BK$):

(Действительно, так как в параллелограмме противоположные стороны параллельны, то $\angle KAD=\angle AKB$ при $AD\parallel BC$ и секущей $AK$. Следовательно, $\angle AKB=\angle KAD=\angle BAK$, откуда следует, что $\triangle ABK$ равнобедренный.)

Значит, $AB=7$. Но у параллелограмма противоположные стороны равны, следовательно, его периметр \[P=2(AB+BC)=2(7+7+12)=52.\]

Ответ: 52

Задание 4 #5145

Биссектрисы углов $A$ и $D$ параллелограмма $ABCD$ пересекаются в точке, лежащей на стороне $BC$. Найдите $AB$, если $BC=44$.

Показать решение

Так как противоположные стороны параллелограмма равны, то $BC=AD=44$.

По свойству параллелограмма биссектриса, проведенная из его угла, отсекает от него равнобедренный треугольник, то есть $\triangle ABK$ – равнобедренный ($AB=BK$).
(Действительно, так как в параллелограмме противоположные стороны параллельны, то $\angle KAD=\angle AKB$ при $AD\parallel BC$ и секущей $AK$. Следовательно, $\angle AKB=\angle KAD=\angle BAK$, откуда следует, что $\triangle ABK$ равнобедренный.)
Аналогично $\triangle CDK$ равнобедренный, то есть $CD=CK$.
Но $AB=CD$ как противоположные стороны параллелограмма, следовательно, $BK=AB=CD=CK$. Следовательно, $AB=\frac12BC=\frac12AD=22$.

Ответ: 22

Задание 5 #5146

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно $15$, а одна из диагоналей ромба равна $60$. Найдите углы ромба.

Показать решение

Пусть $AC=60$. Так как диагонали ромба точкой пересечения делятся пополам, то $AO=OC=30$. Пусть $OH=15$ – расстояние от точки пересечения диагоналей до стороны.

Рассмотрим прямоугольный $\triangle AOH$. Так как катет $OH$ равен половине гипотенузы $AO$, то $\angle HAO=30^\circ$.
Диагонали ромба взаимно перпендикулярны, следовательно, $\angle AOB=90^\circ$. Следовательно, $\angle ABO=90^\circ-\angle BAO=60^\circ$.
Диагонали ромба также являются биссектрисами его углов, следовательно, $\angle BAD=2\angle BAO=60^\circ$, $\angle ABC=2\angle ABO=120^\circ$.

Ответ: 60∘, 120∘, 60∘, 120∘.

Задание 6 #5147

Высота $AH$ ромба $ABCD$ делит сторону $CD$ на отрезки $DH=8$ и $CH=2$. Найдите высоту ромба.

Показать решение

Так как у ромба все стороны равны, то $AD=CD=10$. Рассмотрим прямоугольный $\triangle AHD$. По теореме Пифагора из него $AH=\sqrt{AD^2-HD^2}=\sqrt{10^2-8^2}=6$.

Ответ: 6

Задание 7 #5148

Биссектрисы углов $A$ и $B$ при боковой стороне $AB$ трапеции $ABCD$ пересекаются в точке $F$. Найдите $AB$, если $AF=24$, $BF=10$.

Показать решение

Биссектрисы односторонних углов при двух параллельных прямых перпендикулярны, следовательно, $\angle AFB=90^\circ$.
(Действительно, так как $AD\parallel BC$, то односторонние углы $\angle BAD$ и $\angle ABC$ в сумме дают $180^\circ$ (при секущей $AB$). Так как $AF$, $BF$ – биссектрисы, то $\angle BAF+\angle ABF=0,5(\angle BAD+\angle ABC)=0,5\cdot 180^\circ=90^\circ$.)

Значит, $\triangle ABF$ прямоугольный и по теореме Пифагора \[AB=\sqrt{AF^2+BF^2}=\sqrt{24^2+10^2}=26\]

Ответ: 26