18. Площади геометрических фигур
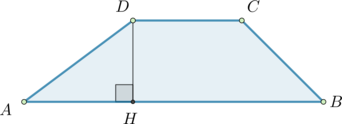
Найдите площадь прямоугольной трапеции, основания которой равны \(6\) и \(2\), большая боковая сторона составляет с основанием угол \(45^\circ\).
Проведем высоту \(CH\).
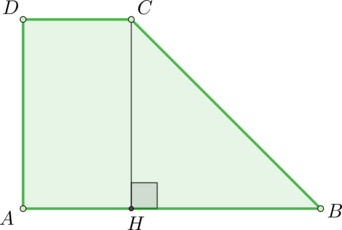
Так как \(\angle HBC=45^\circ\), то \(\angle HCB=45^\circ\). Следовательно, \(\triangle HBC\) равнобедренный и \(HB=HC\).
\(ADCH\) – прямоугольник, следовательно, \(AH=DC=2\). Тогда \(CH=HB=6-2=4\). Тогда площадь трапеции равна \[S=\dfrac{AB+DC}2\cdot CH=\dfrac{2+6}2\cdot 4=16\]
Ответ: 16
Основания прямоугольной трапеции равны \(12\) и \(4\). Ее площадь равна \(64\). Найдите острый угол этой трапеции. Ответ дайте в градусах.
Проведем высоту \(CH\).
\(ADCH\) – прямоугольник, следовательно, \(AH=DC=4\). Тогда \(HB=12-4=8\). Площадь трапеции равна \[64=\dfrac{AB+DC}2\cdot CH=\dfrac{4+12}2\cdot CH\quad\Rightarrow\quad
CH=8\] Заметим, что мы получили, что \(CH=HB=8\). То есть \(\triangle
CHB\) равнобедренный, значит, углы при основании равны, то есть \(\angle HCB=\angle HBC\). Так как сумма острых углов в прямоугольном треугольнике равна \(90^\circ\), то \(\angle B=\angle
HBC=90^\circ:2=45^\circ\).
Ответ: 45
Основания трапеции равны \(18\) и \(6\), боковая сторона, равная \(7\), образует с одним из оснований угол \(150^\circ\). Найдите площадь трапеции.
Пусть \(AD=7\), тогда \(\angle ADC=150^\circ\). По свойству трапеции \(\angle DAB=180^\circ-150^\circ=30^\circ\). Проведем \(DH\perp
AB\).
Рассмотрим \(\triangle ADH\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(DH=AD:2=3,5\). Тогда площадь трапеции равна \[S=\dfrac{AB+DC}2\cdot DH=\dfrac{18+6}2\cdot 3,5=42\]
Ответ: 42
Основания трапеции равны \(27\) и \(9\), боковая сторона равна \(8\). Площадь трапеции равна \(72\). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Пусть \(AD=8\). Проведем \(DH\perp AB\).
Тогда площадь трапеции равна \[72=\dfrac{AB+DC}2\cdot DH=\dfrac{27+9}2\cdot DH\quad\Rightarrow\quad
DH=4\] Рассмотрим прямоугольный \(\triangle ADH\). Так как катет \(DH\) равен половине гипотенузы \(AD\), то угол \(DAH\) равен \(30^\circ\).
Ответ: 30
Основания равнобедренной трапеции равны \(14\) и \(26\), а ее боковые стороны равны \(10\). Найдите площадь трапеции.
Проведем высоту \(BH\). По свойству равнобедренной трапеции \(AH=(AD-BC):2=(26-14):2=6\).
Тогда из прямоугольного треугольника \(ABH\): \[BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-6^2}=8\] Тогда площадь трапеции: \[S=\dfrac{AD+BC}2\cdot BH=\dfrac{26+14}2\cdot 8=160\]
Ответ: 160
Основания равнобедренной трапеции равны \(7\) и \(13\), а ее площадь равна \(40\). Найдите боковую сторону трапеции.
Проведем высоту \(BH\).
Площадь трапеции равна \[40=\dfrac{AD+BC}2\cdot BH=\dfrac{7+13}2\cdot BH\quad\Rightarrow\quad BH=
4\] Рассмотрим прямоугольный \(\triangle ABH\). По свойству равнобедренной трапеции \(AH=(AD-BC):2=(13-7):2=3\). Следовательно, \[AB=\sqrt{AH^2+BH^2}=5\]
Ответ: 5
Основания равнобедренной трапеции равны \(14\) и \(26\), а ее периметр равен \(60\). Найдите площадь трапеции.
Проведем высоту \(BH\). По свойству равнобедренной трапеции \(AH=(AD-BC):2=(26-14):2=6\).
Так как периметр трапеции равен \(60\), а боковые стороны равны, то \[AB=\dfrac{60-14-26}2=10\] Тогда из прямоугольного треугольника \(ABH\): \[BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-6^2}=8\] Тогда площадь трапеции: \[S=\dfrac{AD+BC}2\cdot BH=\dfrac{26+14}2\cdot 8=160\]
Ответ: 160
