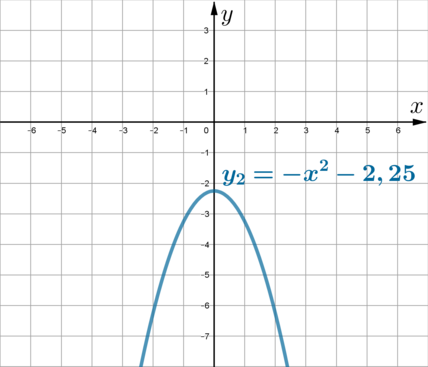
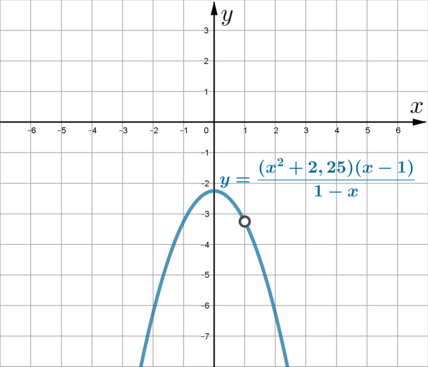
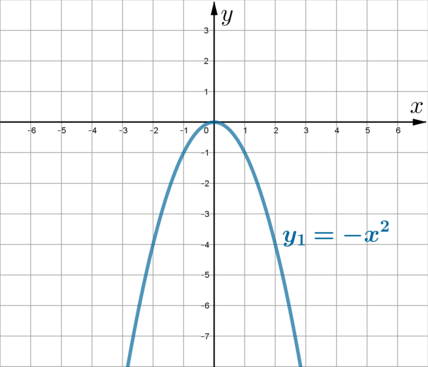
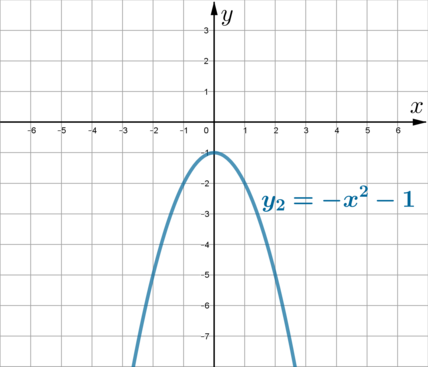
Постройте график функции \[y=4-\dfrac{x+1}{x^2+x}\,.\]
Определите, при каких значениях \(m\) прямая \(y=m\) не имеет с графиком общих точек.
ОДЗ функции: \(x^2+x\ne 0\), откуда \(x\ne -1;0\). При этих значениях \(x\) функцию можно переписать в виде \[y=4-\dfrac1x\quad (x\ne -1)\] Таким образом, нам нужно изобразить график преобразованной функции и выколоть точку с абсциссой \(x=-1\).
Графиком данной функции является гипербола.
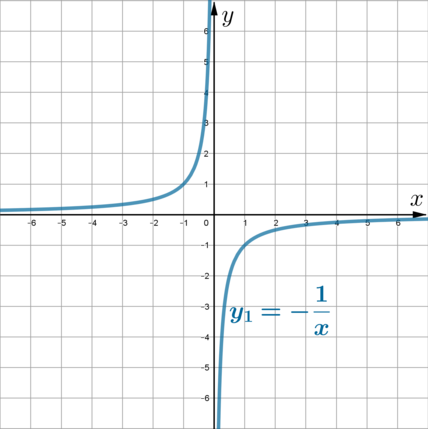
Изображать график будем следующим образом: \[y_1=-\dfrac 1x \ \rightarrow \ y_2=-\dfrac1x +4\] График \(y_1\) – это стандартная гипербола, находящаяся во 2 и 4 четвертях:
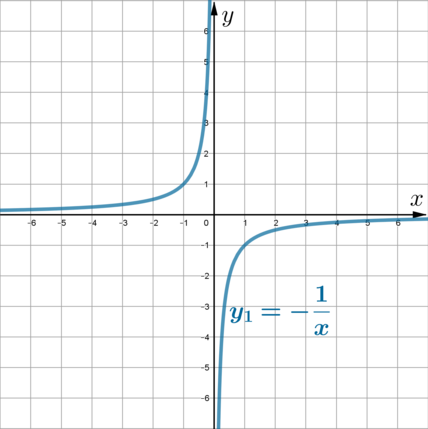
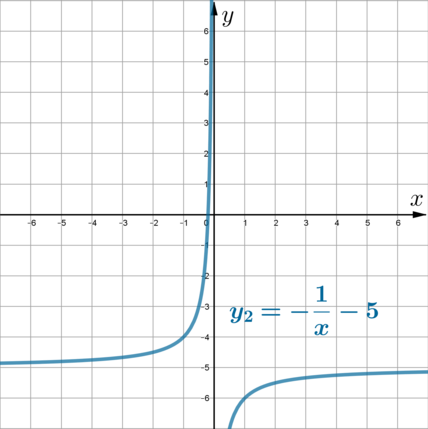
Чтобы получить график функции \(y_2\) из графика функции \(y_1\), нужно поднять график \(y_1\) на 4 единицы вверх (по оси \(Oy\)):
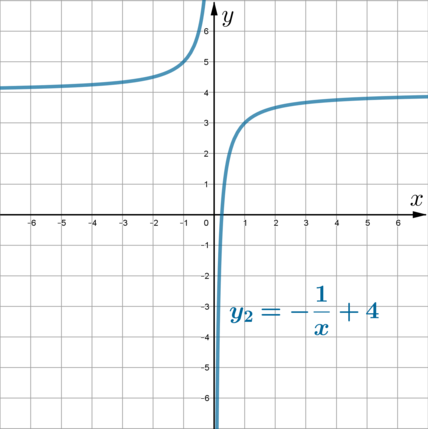
(если у графика \(y_1\) горизонтальная асимптота совпадала с осью \(Ox\), то у графика \(y_2\) она совпадает с прямой \(y=4\))
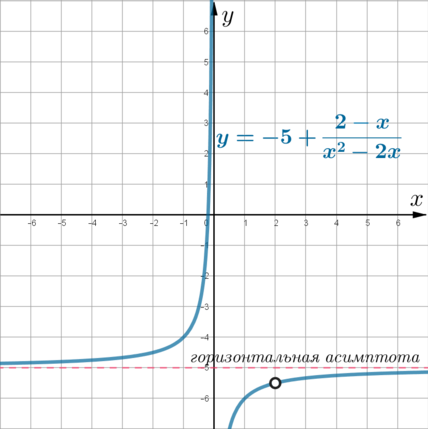
Осталось выколоть точку \((-1; 5)\) и мы получим график функции \(y\):
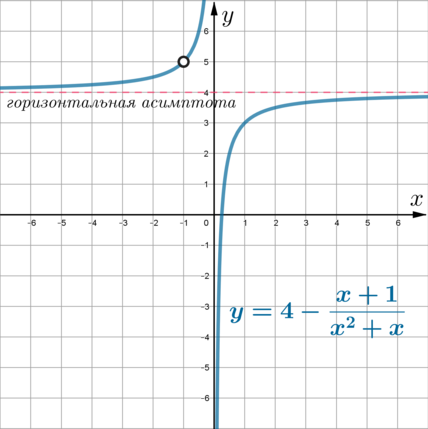
Следовательно, горизонтальная прямая \(y=m\) не имеет с графиком \(y\) общих точек, когда либо совпадает с горизонтальной асимптотой, либо проходит через точку \((-1;5)\). Следовательно, это либо \(y=4\), либо \(y=5\).
Ответ: 4; 5