Постройте график функции \[y=\dfrac{(x^2+3x)\cdot |x|}{x+3}\, .\]
Определите, при каких значениях \(m\) прямая \(y=m\) не имеет с графиком ни одной общей точки.
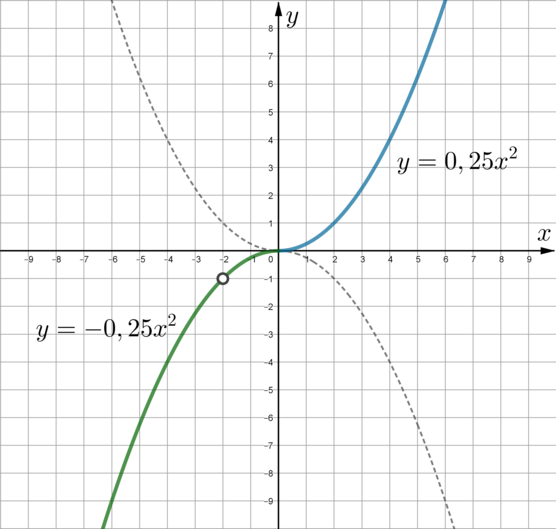
Данную функцию можно преобразовать к виду \[y=\dfrac{x(x+3)\cdot |x|}{x+3}=x\cdot |x| \quad (x+3\ne 0)\]
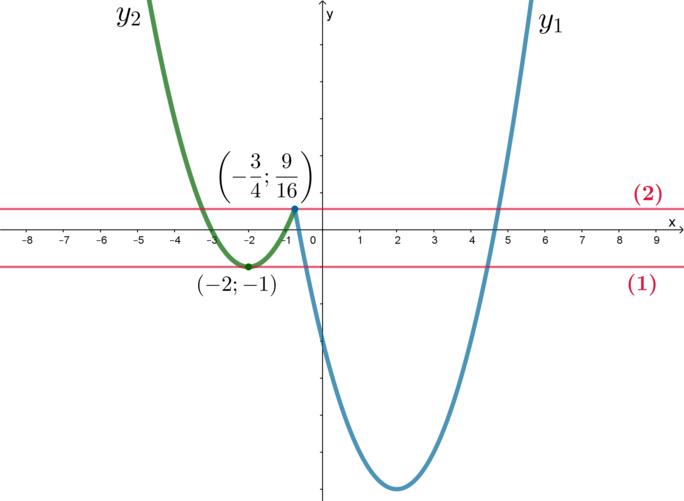
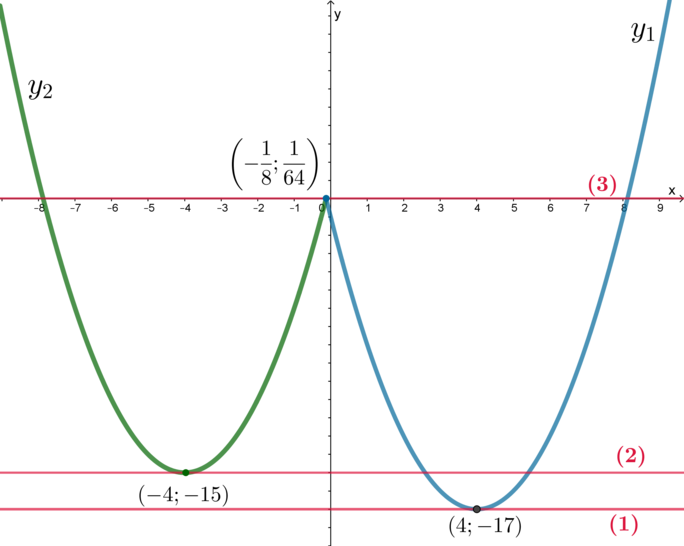
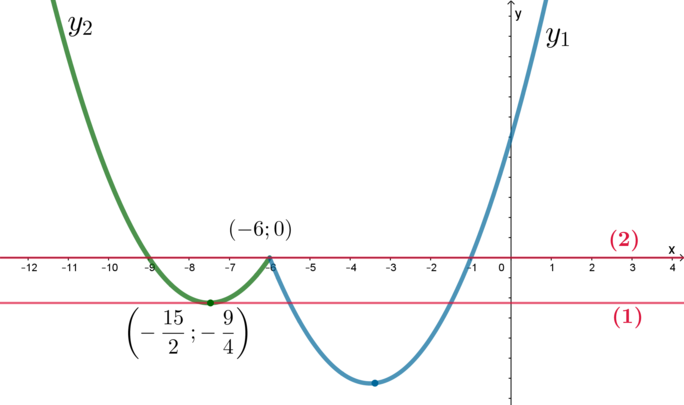
Следовательно, нужно изобразить график функции \(y=x|x|\) и выколоть на нем точку с абсциссой \(x=-3\).
При \(x\geqslant 0\) данная функция примет вид \(y=x\cdot x=x^2\), при \(x<0\): \(y=x\cdot (-x)=-x^2\). Следовательно, получаем кусочно-заданную функцию: \[y=\begin{cases} x^2, \quad x\geqslant 0,\\ -x^2, \quad x<0, x\ne -3. \end{cases}\]
Изобразим:
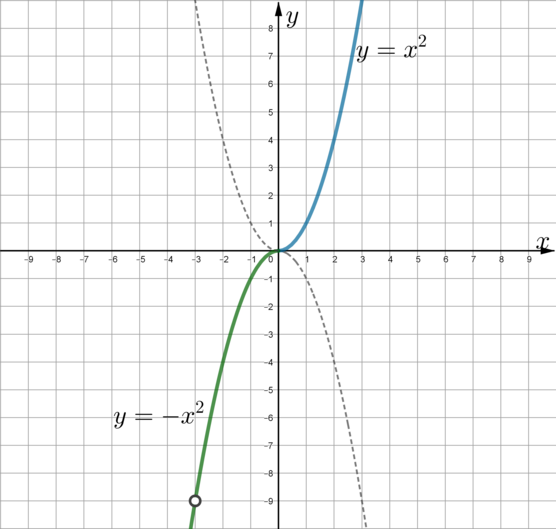
Прямая \(y=m\) – горизонтальная прямая. Единственный случай, когда эта прямая не будет иметь общих точек с графиком данной функции – если она будет проходить через выколотую точку \((-3;-9)\). Следовательно, ее вид будет \(y=-9\), то есть \(m=-9\).
Ответ: -9