Задачи на использование дополнительного построения

Так как \(K\) – середина боковой стороны трапеции, то сразу вспоминаем про среднюю линию трапеции. Поэтому проведем \(KM\) – среднюю линию. Тогда \(KM\parallel AD\).



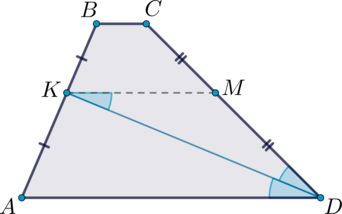
Тогда \(\angle MKD=\angle ADK\) как накрест лежащие при секущей \(KD\) и \(AD\parallel KM\). Отсюда следует, что \(\triangle KMD\) равнобедренный и \(KM=MD=0,5CD=5\). Так как \(KM\) – средняя линия, то она равна полусумме оснований, откуда \(0,5(BC+AD)=5\), значит, \(AD=8\).
Теперь дело за малым, так как если у трапеции известны все стороны, то можно стандартным способом найти ее высоту. Проведем \(BL\perp AD, CH\perp AD\) и введем обозначения, как на рисунке:



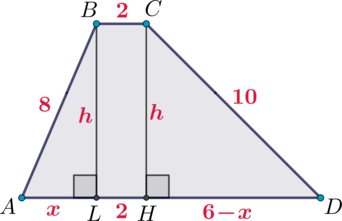
Тогда по теореме Пифагора из \(\triangle ABL\) и \(\triangle DCH\): \(h^2=8^2-x^2\) и \(h^2=10^2-(6-x)^2\), следовательно, \[8^2-x^2=10^2-(6-x)^2\quad\Rightarrow\quad x=0\] Следовательно, точки \(A\) и \(L\) совпадают, то есть \(AB\perp AD\) (трапеция прямоугольная). Значит, \(AB\) и есть высота трапеции. Следовательно, площадь \[S_{ABCD}=\dfrac{AD+BC}2\cdot AB=\dfrac{2+8}2\cdot 8=40.\]

Ответ: 40

Пусть углы при основании \(AD\) равны \(77^\circ\) и \(13^\circ\). Если продолжить боковые стороны трапеции до пересечения в точке \(O\), то \(\angle AOD=180^\circ-77^\circ-13^\circ=90^\circ\).



В прямоугольном \(\triangle BOC\) \(ON\) – медиана, проведенная из вершины прямого угла, следовательно, она равна половине гипотенузы, то есть \(ON=0,5 BC\). Аналогично \(OM=0,5 AD\). \(*\) Следовательно, \(MN=0,5(AD-BC)\). Так как \(KP\) по построению средняя линия, то она равна \(KP=0,5(AD+BC)\). Так какой из отрезков \(KP\) и \(MN\) равен \(11\), а какой \(10\)? Очевидно, что полусумма двух положительных чисел больше их полуразности. Следовательно, \(KP>MN\). Получаем систему \[\begin{cases} 0,5(AD+BC)=11\\ 0,5(AD-BC)=10 \end{cases} \quad\Rightarrow\quad \begin{cases} AD=21 \\ BC=1 \end{cases}\]

\(*\) – здесь еще также нужно доказать, что точки \(O, N, M\) лежат на одной прямой. Так как \(BC\parallel AD\), то \(\angle OCN=\angle ODM\) как соответственные. Медиана, опущенная из вершины прямого угла треугольника, делит его на два равнобедренных треугольника (свойство). Следовательно, \(\angle CON=\angle OCN\) и \(\angle DOM=\angle ODM\). Отсюда \(\angle CON=\angle DOM\). Следовательно, прямые \(ON\) и \(OM\) наклонены к прямой \(OD\) под одинаковым углом, значит, эти прямые совпадают, то есть точки \(O, N, M\) лежат на одной прямой.

Ответ: 21 и 1

Пусть \(AC=4\), \(BD=3\). Сделаем дополнительное построение: проведем \(CK\parallel BD\).



Тогда \(BCKD\) – параллелограмм, следовательно, \(CK=3\), \(DK=BC\). Следовательно, \(AK=AD+BC\). Так как средняя линия равна полусумме оснований, то сумма оснований равна \(5\), значит, \(AK=5\). Посмотрим на \(\triangle ACK\). Его стороны равны \(3, 4, 5\). Следовательно, он прямоугольный, то есть \(\angle ACK=90^\circ\). Отсюда следует, что \(AC\perp CK\), следовательно, \(AC\perp BD\).
Площадь четырехугольника равна полупроизведению диагоналей на синус угла между ними, \(\sin90^\circ=1\), значит, \[S_{ABCD}=\dfrac12AC\cdot BD=\dfrac12\cdot 4\cdot 3=6.\]

Ответ: 6