Задачи с окружностями

Задание 1 #5235

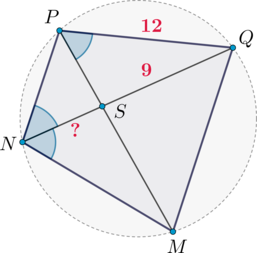
В выпуклом четырехугольнике $NPQM$ диагональ $NQ$ является биссектрисой угла $PNM$ и пересекается с диагональю $PM$ в точке $S$. Найдите $NS$, если известно, что около четырехугольника $NPQM$ можно описать окружность, $PQ=12$, $SQ=9$.

Показать решение

Опишем около четырехугольника $NPQM$ окружность. Углы $PNQ$ и $MNQ$ равны, так как $NQ$ – биссектриса, углы $MNQ$ и $MPQ$ - вписанные, опирающиеся на одну и ту же дугу, следовательно, также равны. Тогда $\triangle NPQ\sim \triangle PSQ$ по двум углам ($\angle PNQ=\angle SPQ$, $\angle NQP$ общий).

Следовательно, \[\dfrac{NQ}{PQ}=\dfrac{PQ}{SQ}\quad\Rightarrow\quad NQ=12^2:9=16\quad\Rightarrow\quad NS=NQ-SQ=7.\]

Ответ: 7

Задание 2 #5236

В равнобедренную трапецию, периметр которой равен $120$, а площадь равна $540$, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до ее меньшего основания.

Показать решение

Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон одинаковы. Следовательно, $AD+BC=AB+CD=P_{ABCD}:2=60$. Так как $AB=CD$, то $AB=30$.
Используя площадь трапеции, можно найти ее высоту: $S_{ABCD}=(AD+BC):2\cdot h=30h$, следовательно, $h=540:30=18$.
Проведем через точку $O$ прямую $HT\perp AD$ и через точку $B$ высоту $BK$:

$OH$ – искомое расстояние. По свойству трапеции $\triangle BOC\sim \triangle AOD$, следовательно, из этого подобия можно найти $OH$. Для этого необходимо найти $AD:BC$.
Рассмотрим $\triangle ABK$. По свойству равнобедренной трапеции $AK=(AD-BC):2$. По теореме Пифагора из этого треугольника \[AK=\sqrt{30^2-18^2}=24.\] Значит, $(AD-BC):2=24$, $(AD+BC):2=30$, откуда $AD=54$, $BC=6$. Следовательно, $AD:BC=9:1$. Значит, $OT:OH=9:1=9x:x$. Так как $10x=HT=18$, то получаем, что $OH=\frac1{10}HT=1,8$.

Ответ: 1,8

Задание 3 #5237

В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основанию $BC$. Окружность проходит через точки $C$ и $D$ и касается прямой $AB$ в точке $E$. Найдите расстояние от точки $E$ до прямой $CD$, если $AD=9$, $BC=4$.

Показать решение

Проведем $EH\perp CD$ – искомое расстояние. Так как угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то $\angle BEC=0,5\buildrel\smile\over{EC}$. Также $\angle CDE=0,5\buildrel\smile\over{EC}$ как вписанный угол. Следовательно, $\angle BEC=\angle CDE$. Аналогично $\angle AED=\angle DCE$.

Следовательно, $\triangle EBC\sim \triangle DHE$ и $\triangle CHE\sim \triangle EAD$ по двум углам. Из полученных подобий следует, что \[\dfrac{BC}{EH}=\dfrac{EC}{ED}\quad \text{и}\quad \dfrac{AD}{EH}=\dfrac{ED}{EC}\] Перемножая эти равенства, получим \[\dfrac{BC\cdot AD}{EH^2}=1\quad\Rightarrow\quad EH=\sqrt{9\cdot 4}=6.\]

Ответ: 6

Задание 4 #5238

Биссектриса $CM$ треугольника $ABC$ делит сторону $AB$ на отрезки $AM=4$, $BM=3$. Касательная к описанной около треугольника $ABC$ окружности, проходящая через точку $C$, пересекает прямую $AB$ в точке $D$. Найдите $CD$.

Показать решение

Рассмотрим чертеж:

По теореме $\triangle BCD\sim \triangle CAD$ (действительно, $\angle D$ – общий, $\angle BCD$ – угол между касательной и хордой, проходящей через точку касания, поэтому равен половине дуги $BC$; $\angle BAC$ равен половине дуги $BC$, как вписанный; следовательно, $\angle BCD=\angle BAC$).
Тогда \[\dfrac{BC}{AC}=\dfrac{BD}{CD}=\dfrac{CD}{AD}\] Так как $CM$ – биссектриса, то $BC:AC=BM:AM=3:4$, следовательно, из данных равенств следует, что $3:4=BD:CD$ и $CD^2=BD\cdot (BD+7)$. Из полученных равенств находим, что \[CD^2=\dfrac34CD\cdot \left(\dfrac34CD+7\right)\quad\Rightarrow\quad CD=12.\]

Ответ: 12

Задание 5 #5239

На стороне $BC$ остроугольного треугольника $ABC$ ($AB\ne AC$) как на диаметре построена полуокружность, пересекающая высоту $AD$ в точке $M$, $AD=10$, $MD=6$, $H$ – точка пересечения высот треугольника $ABC$. Найдите $AH$.

Показать решение

Пусть $N$ – точка пересечения полуокружности и $AC$. Так как $BC$ – диаметр, то $\angle BNC=90^\circ$ как вписанный и опирающийся на диаметр угол. Следовательно, точка пересечения $BN$ и $AD$ – точка $H$. Аналогично $\angle BMC=90^\circ$.

Рассмотрим $\triangle BHD$ и $\triangle ACD$. Они подобны по двум углам (один угол прямой, $\angle BHD=\angle AHN=90^\circ-\angle CAD=\angle ACD$). Следовательно, $HD:DC=BD:AD$, то есть $10HD=BD\cdot DC$.
Так как $\triangle BMC$ прямоугольный и $MD$ – высота из прямого угла, то $6^2=MD^2=BD\cdot DC$. Из полученных двух равенств следует, что $10HD=6^2$, то есть $HD=3,6$. Тогда $AH=10-3,6=6,4$.

Ответ: 6,4

Задание 6 #5240

Точки $M$ и $N$ лежат на стороне $AC$ треугольника $ABC$ на расстояниях соответственно $4$ и $15$ от вершины $A$. Найдите радиус окружности, проходящей через точки $M$ и $N$ и касающейся луча $AB$, если $\cos \angle BAC=\frac{\sqrt{15}}4$.

Показать решение

Проведем $KM$ и $KN$ ($K$ – точка касания окружности и $AB$). Так как угол между касательной и хордой, проведенной в точку касания, равен вписанному углу, опирающемуся на дугу, заключенную между касательной и хордой, то $\angle AKM=\angle KNM=\beta$. Обозначим $\angle BAC=\alpha$.

Будем искать радиус $R$ по теореме синусов: $2R=\frac{KM}{\sin \beta}$. Найдем $\beta$ и $KM$.
Так как $AK$ – касательная, $AN$ – секущая, то $AK^2=AM\cdot AN=4\cdot 15$, откуда $AK=2\sqrt{15}$. Тогда по теореме косинусов из $\triangle AKM$: \[KM^2=AK^2+AM^2-2AK\cdot AM\cdot \cos\alpha=16\quad\Rightarrow\quad KM=4.\] Следовательно, $\triangle AKM$ равнобедренный ($AM=KM=4$), то есть $\alpha=\beta$.
Так как $\cos \alpha=\frac{\sqrt{15}}4$, то $\sin\alpha=\sqrt{1-\cos^2\alpha}=\sqrt{1-\frac{15}{16}}=\frac14$. Следовательно, \[2R=\dfrac{4}{\frac14}\quad\Rightarrow\quad R=8.\]

Ответ: 8

Задание 7 #5241

В треугольнике $ABC$ известно, что $AB=2$, $AC=6$, точка $O$ – центр окружности, описанной около треугольника $ABC$. Прямая $BD$, перпендикулярная прямой $AO$, пересекает сторону $AC$ в точке $D$. Найдите $CD$.

Показать решение

Если радиус окружности перпендикулярен хорде, то он делит ее пополам. Следовательно, $BQ=QL$ (см. рисунок). Так как $AQ$ – медиана и высота в $\triangle ABL$, то он равнобедренный, следовательно, $\angle ALB=\angle ABL$. $\angle ALB=\angle ACB$ как вписанные, опирающиеся на одну и ту же дугу.

Следовательно, $\angle ACB=\angle ABL$. Тогда по двум углам (другой $\angle BAC$ – общий) треугольники $ABC$ и $ADB$ подобны. Следовательно, \[\dfrac{AB}{AD}=\dfrac{AC}{AB}\quad\Rightarrow\quad AB^2=AC\cdot AD \quad\Rightarrow\quad 4=6\cdot (6-CD)\quad\Rightarrow\quad CD=\dfrac{16}3.\]

Ответ: $\frac{16}3$