Задачи с окружностями (страница 2)

Задание 8 #5242

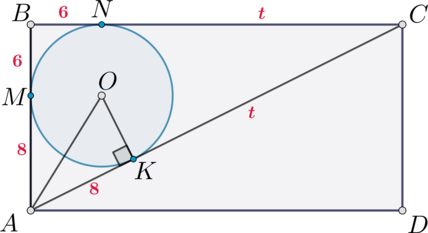
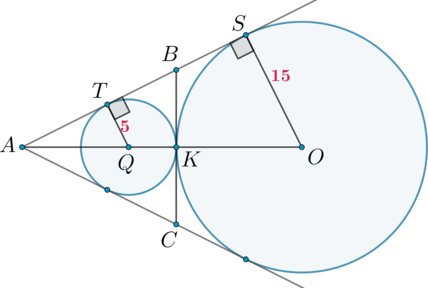
Окружности радиусов $1$ и $4$ касаются внешним образом. Точки $A$ и $B$ лежат на первой окружности, точки $C$ и $D$ – на второй. При этом $AC$ и $BD$ – общие касательные окружностей. Найдите расстояние между прямыми $AB$ и $CD$.

Показать решение

1) Докажем, что прямая, соединяющая центры окружностей, перпендикулярна $AB$ и $CD$ и что $AB\parallel CD$.
Пусть касательные $AC$ и $BD$ пересекаются в точке $M$:

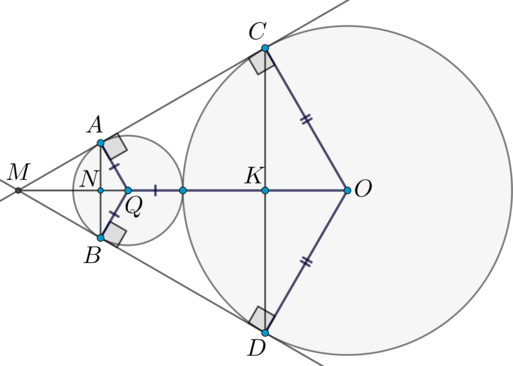
Так как радиус, проведенный в точку касания, перпендикулярен касательной, то $\angle MCO=\angle MDO=90^\circ$. $\triangle MCO=\triangle MDO$ как прямоугольные по общей гипотенузе и катету. Следовательно, $\angle MOC=\angle MOD$. Тогда в равнобедренном $\triangle COD$ $OK$ – биссектриса, следовательно, медиана и высота. То есть $OK\perp CD$. Аналогично доказывается, что $QN\perp AB$. Так как отрезки $OK$ и $QN$ лежат на прямой $QO$, то $QO\perp AB, QO\perp CD$. Следовательно, $AB\parallel CD$.

Таким образом, расстояние между прямыми $AB$ и $CD$ – длина отрезка $NK=QO+QN-OK$.

2) $QO$ равно сумме радиусов окружностей, то есть $QO=5$. Проведем $QH\perp CO$.

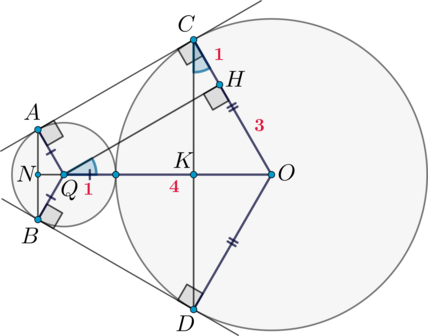
Тогда $ACHQ$ – прямоугольник, следовательно, $CH=1$, откуда $HO=4-1=3$. Заметим, что $\triangle QOH\sim \triangle COK$ по двум углам (прямой и общий), следовательно, \[\dfrac{CO}{QO}=\dfrac{KO}{HO}\quad\Rightarrow\quad KO=\dfrac{4\cdot 3}5= \dfrac{12}5\] $\triangle COK\sim \triangle AQN$ (по прямому углу и $\angle AQN=\angle COK$ как соответственные при $AQ\parallel CO$ и $NO$ секущей). Следовательно, \[\dfrac{AQ}{CO}=\dfrac{NQ}{KO}\quad\Rightarrow\quad NQ=\dfrac{1\cdot \frac{12}5}4= \dfrac35\] Следовательно, $NK=5-\frac{12}5+\frac35=\frac{16}5=3,2$.

Ответ: 3,2

Задание 9 #5243

На стороне $AB$ треугольника $ABC$ взята точка $D$ так, что окружность, проходящая через точки $A, C, D$, касается прямой $BC$. Найдите $AD$, если $AC=9$, $BC=12$, $CD=6$.

Показать решение

Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними. То есть $\angle BCD=0,5\buildrel\smile\over{CD}$, так же как и $\angle CAD$ (вписанный).

Следовательно, по двум углам ($\angle ABC$ – общий) $\triangle BCD\sim \triangle BAC$, откуда \[\dfrac{BC}{AB}=\dfrac{CD}{AC}=\dfrac{BD}{BC}\quad\Rightarrow\quad \dfrac{12}{AB}=\dfrac69=\dfrac{BD}{12}\] Из полученных равенств можно найти $AB=18$ и $BD=8$. Следовательно, $AD=18-8=10$.

Ответ: 10

Задание 10 #5244

Четырехугольник $ABCD$ со сторонами $AB=3$, $CD=5$ вписан в окружность. Диагонали $AC$ и $BD$ пересекаются в точке $K$, причем $\angle AKB=60^\circ$. Найдите радиус окружности, описанной около этого четырехугольника.

Показать решение

Как известно, если хорды окружности пересекаются, то они образуют пары подобных треугольников, то есть $\triangle ABK\sim \triangle DCK$ ($\angle AKB=\angle DKC$ – вертикальные, $\angle ABK=\angle DCK$ – вписанные, опирающиеся на одну и ту же дугу). Следовательно, \[\dfrac35=\dfrac{AB}{CD}=\dfrac{BK}{CK}\] Значит, можно обозначить $BK=3x$, $CK=5x$.

Заметим, что $\angle BKC=180^\circ-60^\circ=120^\circ$. Тогда по теореме косинусов из $\triangle BKC$: \[BC^2=BK^2+CK^2-2\cdot BK\cdot CK\cdot \cos 120^\circ \quad\Rightarrow\quad BC=7x\] Тогда по теореме синусов для $\triangle BKC$: \[\dfrac{BC}{\sin 120^\circ}=\dfrac{BK}{\sin \angle BCA} \quad\Rightarrow\quad \sin \angle BCA=\dfrac{3\sqrt3}{14}\] Следовательно, по теореме синусов для $\triangle ABC$ (он является вписанным в данную окружность) \[2R=\dfrac{AB}{\sin \angle BCA}\quad\Rightarrow\quad R=\dfrac7{\sqrt{3}}\]

Ответ: $\dfrac7{\sqrt{3}}$

Задание 11 #5245

В параллелограмме $ABCD$ проведена диагональ $AC$. Точка $O$ является центром окружности, вписанной в треугольник $ABC$. Расстояния от точки $O$ до точки $A$ и прямых $AD$ и $AC$ соответственно равны $10$, $8$ и $6$. Найдите площадь параллелограмма $ABCD$.

Показать решение

Пусть $M, N, K$ – точки касания окружности со сторонами $\triangle ABC$.
Заметим, что числа $6, 8, 10$ – пифагорова тройка. Следовательно, $AK=8$, $AH=6$.
Заметим, что $OK$ — и расстояние от центра окружности до $AC$, и радиус окружности, следовательно, $ON=6$. Так как $AD\parallel BC$, то из $OH\perp AD$ и $ON\perp BC$ следует, что $N, O, H$ лежат на одной прямой, то есть $NH$ – высота параллелограмма, то есть $h=NH=8+6=14$.
$AM=AK=8$ как отрезки касательных, проведенных из одной точки к окружности, аналогично $BM=BN=x$.

Проведем $BT\perp AD$, $BT=h=14$. Так как $BNHT$ – прямоугольник, то $TH=BN=x$. Следовательно, в прямоугольном $\triangle ABT$: $AB=8+x$, $BT=14$, $AT=6-x$. Тогда \[(8+x)^2=14^2+(6-x)^2\quad\Rightarrow\quad x=6.\] Это значит, что $AT=0$, то есть точки $A$ и $T$ совпадают. А это в свою очередь значит, что $ABCD$ – прямоугольник.

Как отрезки касательных, проведенных из одной точки к окружности, равны $CN=CK=t$. Тогда из прямоугольного $\triangle ABC$: \[(8+t)^2=14^2+(6+t)^2\quad\Rightarrow\quad t=42.\] Следовательно, $BC=6+42=48$ и $S_{ABCD}=14\cdot 48=672$.

Ответ: 672

Задание 12 #5246

Середина $M$ стороны $AD$ выпуклого четырехугольника $ABCD$ равноудалена от всех его вершин. Найдите $AD$, если $BC=4$, а углы $B$ и $C$ четырехугольника равны соответственно $128^\circ$ и $112^\circ$.

Показать решение

То, что $M$ равноудалена от $A, B, C, D$, означает, что можно провести окружность с центром в точке $M$ и радиуса $MA$ и точки $B, C, D$ будут также лежать на этой окружности.

Таким образом, четырехугольник $ABCD$ вписанный. У вписанного четырехугольника сумма противоположных углов равна $180^\circ$, откуда $\angle D=180^\circ-128^\circ=52^\circ$, $\angle A=180^\circ-112^\circ=68^\circ$. Так как $\triangle AMB$ равнобедренный, то $\angle MBA=68^\circ$, откуда $\angle MBC=128^\circ-68^\circ=60^\circ$. Следовательно, в равнобедренном $\triangle MBC$ один из углов $60^\circ$, то есть он равносторонний. Значит, радиус окружности равен $BC$, то есть $MA=MB=MC=MD=4$, откуда $AD=8$.

Ответ: 8

Задание 13 #5247

В трапеции $ABCD$ основания $AD$ и $BC$ равны соответственно $36$ и $12$, а сумма углов при основании $AD$ равна $90^\circ$. Найдите радиус окружности, проходящей через точки $A$ и $B$ и касающейся прямой $CD$, если $AB=10$.

Показать решение

Рассмотрим чертеж:

Предположим, что окружность касается прямой $CD$ в точке $K$, причем $K$ лежит за точкой $C$.
Если продолжить боковые стороны до пересечения в точке $O$, то $\angle AOD=180^\circ-90^\circ=90^\circ$.
Рассмотрим $\triangle AOD$ и $\triangle BOC$. Они подобны ($\angle O$ общий, $\angle OBC=\angle OAD$ как соответственные при $AD\parallel BC$ и секущей $AB$), следовательно, \[\dfrac{BC}{AD}=\dfrac{OB}{OA}=\dfrac{OB}{OB+10}\quad\Rightarrow\quad OB=5.\] Так как квадрат касательной равен произведению секущей на ее внешнюю часть, то $OK^2=OA\cdot OB=5\cdot 15=75$. Тогда по теореме Пифагора из $\triangle BOK$: $BK=\sqrt{5^2+75}=10$. Следовательно, $\triangle ABK$ (около которого описана данная окружность) является равнобедренным.
Видим, что наше предположение относительно положения точки $K$ оказалось верным, так как $BK<BC$.

Угол $OKB$ между касательной $OK$ и хордой $BK$ равен углу $BAK$. Следовательно, по теореме синусов \[2R=\dfrac{BK}{\sin\angle BAK}=\dfrac{BK}{\sin\angle OKB}\] Найдем $\sin \angle OKB$ из $\triangle OKB$: \[\sin \angle OKB=\dfrac 5{10}=\dfrac12\] Следовательно, \[R=\dfrac{BK}{2\cdot \frac12}=10.\]

Ответ: 10

Задание 14 #5248

Две касающиеся внешним образом в точке $K$ окружности, радиусы которых равны $5$ и $15$, вписаны в угол с вершиной $A$. Общая касательная к этим окружностям, проходящая через точку $K$, пересекает стороны угла в точках $B$ и $C$. Найдите радиус окружности, описанной около $\triangle ABC$.

Показать решение

Рассмотрим чертеж:

Пусть $T$, $S$ – точки касания окружностей со стороной $AB$ угла $A$, $Q$, $O$ – центры окружностей.
Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, следовательно, $AO$ – биссектриса $\angle A$.
Рассмотрим $\triangle ATQ$ и $\triangle ASO$. Они подобны по общему углу $\angle SAO$ и прямому углу. Следовательно, \[\dfrac{AQ}{AO}=\dfrac{TQ}{SO}=\dfrac5{15}\quad\Rightarrow\quad 3AQ=AO\] Так как $AO=AQ+5+15$, то из $3AQ=AO$ находим, что $AQ=10$. Тогда в прямоугольном $\triangle ATQ$ гипотенуза равна $10$, катет равен $5$, следовательно, $\angle TAQ=30^\circ$. Тогда весь $\angle A=60^\circ$.

По теореме Пифагора $AT=\sqrt{10^2-5^2}=5\sqrt3$.
Так как $BC$ – касательная, то $QK\perp BC$, то есть $\triangle AKB$ – прямоугольный. $\triangle ATQ\sim \triangle AKB$, следовательно, \[\dfrac{TQ}{BK}=\dfrac{AT}{AK}\quad\Rightarrow\quad \dfrac5{BK}=\dfrac{5\sqrt3}{10+5}\quad\Rightarrow\quad BK=5\sqrt3.\] Так как картинка симметрична относительно $AO$, то $CK=BK=5\sqrt3$, откуда $BC=10\sqrt3$.
Тогда по теореме синусов для $\triangle ABC$: \[R=\dfrac{BC}{2\sin\angle A}=\dfrac{10\sqrt3}{2\cdot \frac{\sqrt3}2}=10.\]

Ответ: 10