17. Окружность
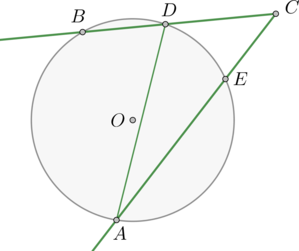
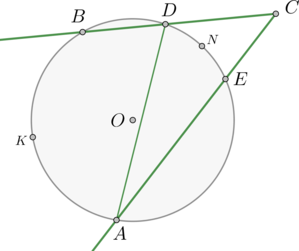
Точки \(A\), \(B\), \(C\) и \(D\) угла \(AOB\) лежат на окружности. Дуга \(AB\), заключённая внутри этого угла, равна \(65^{\circ}\), а дуга \(CD\), заключённая внутри этого угла, равна \(22^{\circ}\). Найдите величину угла \(AOB\). Ответ дайте в градусах.
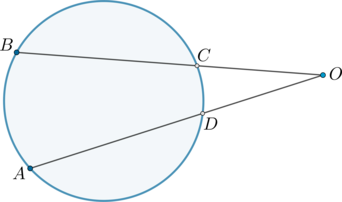
\(\angle AOB\) равен полуразности дуг \(AB\) и \(CD\), заключённых внутри него, тогда \[\angle BOD = 0,5(\buildrel\over{ AB} - \buildrel\over{ CD}) = 0,5(65^{\circ} - 22^{\circ}) = 21,5^{\circ}.\]
Ответ: 21,5
Через концы \(A\) и \(B\) дуги окружности в \(62^\circ\) проведены касательные \(AC\) и \(BC\). Найдите угол \(ACB\). Ответ дайте в градусах.
Так как угол между касательной и хордой, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то \(\angle ABC=\angle BAC=0,5\cdot 62^\circ=31^\circ\). Следовательно, из \(\triangle ABC\): \(\angle ACB=180^\circ-2\cdot 31^\circ=118^\circ\).
Ответ: 118
Угол \(ACO\) равен \(24^\circ\). Его сторона \(CA\) касается окружности с центром в точке \(O\). Найдите градусную меру дуги \(AD\), заключенной внутри этого угла, где \(B\) и \(D\) – точки пересечения секущей \(CO\) с окружностью. Ответ дайте в градусах.
Найдем градусную меру меньшей дуги, стягиваемой хордой \(AB\). Она равна центральному углу \(AOB\), на нее опирающемуся. Так как радиус, проведенный в точку касания, перпендикулярен касательной, то \(\angle OAC=90^\circ\). Следовательно, из \(\triangle OAC\): \(\angle AOC=90^\circ-24^\circ=66^\circ\). Тогда \(\angle AOD=180^\circ-\angle AOC=114^\circ\). Дуга \(AD\), заключенная внутри угла \(ACD\), равна центральному углу \(AOD\) и равна \(114^\circ\).
Ответ: 114
Найдите угол \(ACB\), если вписанные углы \(ADB\) и \(DAE\) опираются на дуги окружности, градусные меры которых равны соответственно \(118^\circ\) и \(38^\circ\). Ответ дайте в градусах.
Так как угол между двумя секущими, проведенными из одной точки вне окружности, равен полуразности дуг, заключенных между ними, то \(\angle ACB=0,5(118^\circ-38^\circ)=40^\circ\).
Ответ: 40
Угол \(ACB\) равен \(42^\circ\). Градусная мера дуги \(AB\) окружности, не содержащей точки \(D\) и \(E\), равна \(124^\circ\). Найдите угол \(DAE\). Ответ дайте в градусах.
Так как угол между двумя секущими, проведенными из одной точки вне окружности, равен полуразности дуг, заключенных между ними, то \(\angle
ACB=0,5(\buildrel\smile\over{AKB}-\buildrel\smile\over{DNE})=42^\circ\). Так как \(\buildrel\smile\over{AKB}=124^\circ\), то \(\buildrel\smile\over{DNE}=124^\circ-2\cdot 42^\circ=40^\circ\). Тогда \(\angle DAE\), как вписанный и опирающийся на дугу \(\buildrel\smile\over{DNE}\), равен ее половине, то есть \(20^\circ\).
Ответ: 20
Прямая \(b\) касается окружности в точке \(B\) и образует с хордой \(AB\) угол, равный \(55^{\circ}\). Найдите градусную меру дуги \(AB\), которая меньше полуокружности. Ответ дайте в градусах.
Угол между касательной и хордой равен половине градусной меры дуги окружности, заключённой внутри него, следовательно градусная мера искомой дуги равна \(2\cdot 55^{\circ} = 110^{\circ}\).
Ответ: 110
\(AC\) – диаметр окружности с центром в точке \(O\). Найдите \(\angle ABC\), если \(B\) лежит на окружности. Ответ дайте в градусах
\(\angle ABC\) – вписанный. Вписанный угол в два раза меньше градусной меры дуги, на которую он опирается.
Градусная мера дуги есть градусная мера центрального угла, который на неё опирается, тогда градусная мера дуги \(AC\) равна \(180^{\circ}\) и \(\angle ABC = 90^{\circ}\).
Ответ: 90
