16. Многоугольники. Базовые свойства
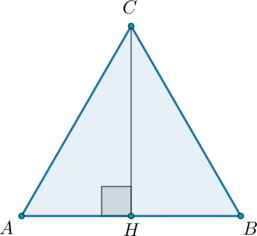
В треугольнике \(ABC\) \(AC=BC=4\), \(\angle C=30^\circ\). Найдите высоту \(AH\).
Рассмотрим прямоугольный \(\triangle ACH\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(AH=0,5AC=2\).
Заметим, что условие \(BC=4\) в данной задаче является лишним.
Ответ: 2
В равностороннем треугольнике \(ABC\) высота \(CH\) равна \(2\sqrt3\). Найдите \(AB\).
Так как \(AC=BC\), то \(CH\) также является медианой. Следовательно, если \(AH=a\), то \(AB=AC=2a\). Тогда по теореме Пифагора из \(\triangle ACH\): \[AC^2=AH^2+CH^2\quad\Rightarrow\quad 4a^2=a^2+12\quad\Rightarrow\quad a=2\quad\Rightarrow\quad AB=2a=4\]
Ответ: 4
В треугольнике \(ABC\) \( \ AB=BC=AC=2\sqrt3\). Найдите высоту \(CH\).
Так как \(AC=BC\), то \(CH\) также является медианой, следовательно, \(AH=0,5 AB=\sqrt3\). Тогда по теореме Пифагора из \(\triangle ACH\): \[CH=\sqrt{AC^2-AH^2}=3\]
Ответ: 3
В треугольнике \(ABC\) угол \(C\) равен \(90^\circ\), \(CH\) – высота, угол \(A\) равен \(30^\circ\). Найдите \(BH\), если \(AB=4\).
Так как катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(BC=0,5AB=2\).
По свойству прямоугольного треугольника \(\angle BCH=\angle
A=30^\circ\), следовательно, из \(\triangle BCH\): \(HB=0,5
BC=1\).
Ответ: 1
В \(\triangle ABC\) \(AH\) – высота, \(BD\) – биссектриса, \(O\) – точка пересечения прямых \(AH\) и \(BD\), угол \(ABD\) равен \(62^\circ\). Найдите угол \(AOB\).
Так как \(BD\) – биссектриса, то \(\angle CBD=\angle ABD= 62^\circ\). \(\angle HBO=\angle CBD=62^\circ\) как вертикальные.
\(\angle OHB=\angle AHB=90^\circ\).
Следовательно, \(\angle AOB=\angle HOB=90^\circ-\angle
HBO=90^\circ-62^\circ=28^\circ\) (так как сумма острых углов в прямоугольном треугольнике равна \(90^\circ\)).
Ответ: 28
В треугольнике \(ABC\) угол \(C\) равен \(90^\circ\), угол \(A\) равен \(30^\circ\), \(AB=2\sqrt3\). Найдите высоту \(CH\).
Так как катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(BC=0,5AB=\sqrt3\).
По свойству прямоугольного треугольника \(\angle BCH=\angle
A=30^\circ\), следовательно, из \(\triangle BCH\): \(HB=0,5
BC=\sqrt3:2\).
Тогда по теореме Пифагора из \(\triangle BCH\): \[CH=\sqrt{BC^2-BH^2}=\sqrt{\dfrac94}=1,5\]
Ответ: 1,5
В треугольнике \(ABC\): \(BM\) – биссектриса, на сторонах \(AB\) и \(BC\) выбраны точки \(P\) и \(Q\) соответственно, причём перпендикуляр к \(AB\), проходящий через точку \(P\) и перпендикуляр к \(BC\), проходящий через точку \(Q\), пересеклись в точке \(K\), лежащей на биссектрисе \(BM\). Найдите \(PK\), если известно, что \(KQ = 33\).
Так как каждая точка биссектрисы угла равноудалена от его сторон, то \(PK = KQ = 33\).
Покажем это подробнее:
треугольники \(PKB\) и \(BKQ\) – прямоугольные, имеющие общую гипотенузу и \(\angle PBK = \angle KBQ\), тогда треугольники \(PKB\) и \(BKQ\) равны по гипотенузе и острому углу, значит, \(PK = KQ\).
Ответ: 33
