16. Многоугольники. Базовые свойства
В параллелограмме \(ABCD\) проведены биссектрисы \(AN\) и \(BM\), \(\angle ABM = 58^{\circ}\). Найдите \(\angle BAN\). Ответ дайте в градусах.
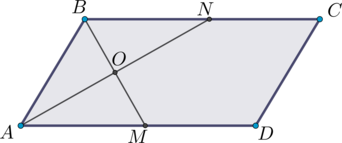
Сумма односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\), тогда \(\angle DAB + \angle ABC = 180^{\circ}\).
Так как \(AN\) и \(BM\) – биссектрисы, то \(\angle BAN + \angle ABM = 0,5(\angle DAB + \angle ABC) = 90^{\circ}\).
\(\angle ABM = 58^{\circ}\), тогда \(\angle BAN = 90^{\circ} - 58^{\circ} = 32^{\circ}\).
Ответ: 32
В параллелограмме \(ABCD\) сумма длин диагоналей равна 10, а меньшая сторона параллелограмма \(ABCD\) равна 2. Найдите наименьший из периметров треугольников, на которые диагонали делят параллелограмм \(ABCD\).
В параллелограмме диагонали пересекаются и точкой пересечения делятся пополам. Пусть точка пересечения диагоналей – точка \(O\), тогда \(AO + BO = 0,5(AC + BD) = 5 = AO + OD = OD + OC = OC + OB\).
Таким образом, периметр каждого из треугольников, на которые диагонали делят параллелограмм \(ABCD\), равен полусумме диагоналей параллелограмма \(ABCD\) плюс сторона параллелограмма, которая является стороной этого треугольника.
Тогда наименьшим будет периметр того из этих треугольников, стороной которого является одна из меньших сторон параллелограмма и равен он \(5 + 2 = 7\).
Ответ: 7
Из точки \(C\) параллелограмма \(ABCD\) опустили перпендикуляр на продолжение стороны \(AD\) за точку \(D\). Этот перпендикуляр пересёк прямую \(AD\) в точке \(E\), причём \(CE = DE\). Найдите \(\angle B\) параллелограмма \(ABCD\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle EDC = \angle DCE\). Так как \(\angle DEC = 90^{\circ}\), а сумма углов треугольника равна \(180^{\circ}\), то \(\angle EDC = 45^{\circ}\), тогда \(\angle ADC = 180^{\circ} - 45^{\circ} = 135^{\circ}\). Так как в параллелограмме противоположные углы равны, то \(\angle B = \angle ADC = 135^{\circ}\).
Ответ: 135
Периметр параллелограмма равен \(15\). При этом одна сторона этого параллелограмма на \(5\) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть \(BC = AB + 5\), тогда периметр параллелограмма \(ABCD\) равен \(AB + BC + CD + AD = AB + AB + 5 + AB + AB + 5 = 4\cdot AB + 10 = 15\), откуда находим \(AB = 1,25\). Тогда меньшая сторона параллелограмма равна \(1,25\).
Ответ: 1,25
Биссектрисы углов \(B\) и \(C\) параллелограмма \(ABCD\) пересекаются на стороне \(AD\). Найдите \(BC\), если \(AB=4\).
По свойству биссектрисы параллелограмма \(\triangle ABK\) и \(\triangle CDK\) – равнобедренные (\(AB=AK\), \(CD=DK\)). Следовательно, \[BC=AD=AK+DK=AB+CD=2AB=8.\]
Ответ: 8
В ромбе \(ABCD\) угол \(DAB\) равен \(148^\circ\). Найдите угол \(BDC\). Ответ дайте в градусах.
Так как в ромбе диагонали являются биссектрисами углов, то \(\angle BDC=\angle BDA\). Так как у ромба все стороны равны, то \(AD=AB\), следовательно, \(\angle BDA=\angle DBA=x\). Тогда \(x+x+\angle DAB=180^\circ\), откуда \[x=(180^\circ-148^\circ):2=16^\circ\]
Ответ: 16
В ромбе \(ABCD\) угол \(CDA\) равен \(78^\circ\). Найдите угол \(ACB\). Ответ дайте в градусах.
Так как в ромбе диагонали являются биссектрисами углов, то \(\angle ACB=\angle ACD\). Так как у ромба все стороны равны, то \(AD=DC\), следовательно, \(\angle CAD=\angle ACD=x\). Тогда \(x+x+\angle CDA=180^\circ\), откуда \[x=(180^\circ-78^\circ):2=51^\circ\]
Ответ: 51
