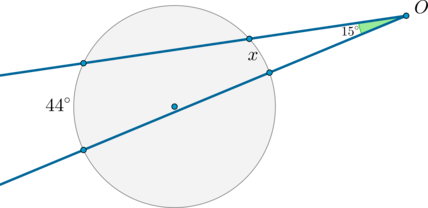
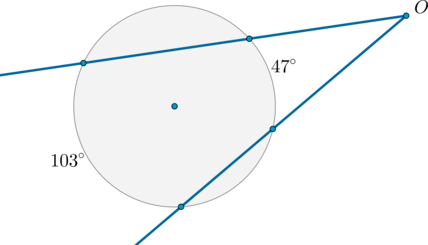
Касательные \(CA\) и \(CB\) к окружности образуют угол \(ACB\), равный \(112^\circ\). Найдите величину меньшей дуги \(AB\), стягиваемой точками касания. Ответ дайте в градусах.
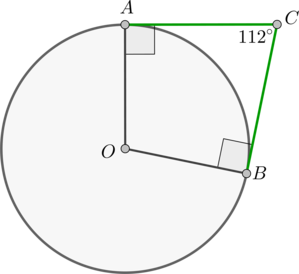
Пусть \(O\) – центр окружности. Проведем радиусы \(OA\) и \(OB\). Так как радиус, проведенный в точку касания, перпендикулярен касательной, то \(OA\perp AC, OB\perp BC\). Заметим, что \(OACB\) – четырехугольник. Так как сумма углов четырехугольника равна \(360^\circ\), то \[\angle AOB=360^\circ-112^\circ-90^\circ-90^\circ=68^\circ.\] \(\angle AOB\) – центральный угол, опирающийся на дугу \(AB\), следовательно, \(\buildrel\smile\over{AB}=\angle AOB=68^\circ\).
Ответ: 68