Вписанная окружность (страница 3)

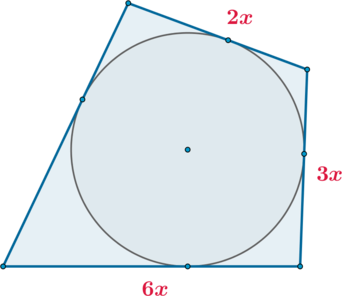
Рассмотрим рисунок. Так как четырехугольник описан около окружности, то суммы его противоположных сторон равны. Следовательно, четвертая сторона равна \((2x+6x)-3x=5x\). Тогда можно составить уравнение: \[2x+3x+6x+5x=54\quad\Leftrightarrow\quad 6x=20,25\] (большая сторона равна \(6x\))

Ответ: 20,25

Рассмотрим рисунок. Пусть \(A_1, B_1, C_1\) – точки касания сторон \(\triangle ABC\) с окружностью. \(A', B', C'\) – точки на окружности, через которые проведены касательные параллельно сторонам треугольника. Получились треугольники \(AMN, BLK, CPR\). Пусть \(P_{AMN}=5, P_{BLK}=6, P_{CPR}=7\).
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то \(MA'=MC_1, NA'=NB_1\). Следовательно, \[P_{AMN}=AM+MA'+NA'+AN=AM+MC_1+NB_1+AN=AC_1+AB_1=5\] Аналогично для других треугольников: \[\begin{aligned} &P_{BLK}=BC_1+BA_1=6\\ &P_{CPR}=CA_1+CB_1=7 \end{aligned}\] Следовательно, \[P_{ABC}=(AC_1+AB_1)+(BC_1+BA_1)+(CA_1+CB_1)=5+6+7=18.\]

Ответ: 18

Пусть дан ромб \(ABCD\), \(AB=8\), \(O\) – центр окружности, вписанной в этот ромб. Т.к. центр окружности, вписанной в многоугольник, лежит на пересечении биссектрис его углов, то \(O\) – точка пересечения диагоналей ромба (т.к. они являются биссектрисами углов ромба). Пусть \(K\) – точка касания окружности со стороной \(AB\). Тогда \(OK=r\) – радиус окружности.

Рассмотрим треугольники \(OKA\) и \(OBA\). Они подобны по двум углам. Следовательно, \[\dfrac{OK}{OB}=\dfrac{OA}{AB} \quad \Rightarrow \quad r=OK=\dfrac{OA\cdot OB}{AB}\]

Т.к. площадь ромба равна полупроизведению диагоналей, то \(S=\frac12\cdot AC\cdot BD=\frac12\cdot 2\,OA\cdot 2\,OB=2\,OA\cdot OB=10\). Отсюда \(OA\cdot OB=5\). Следовательно,

\[r=\dfrac58=0,625.\]

Ответ: 0,625

Рассмотрим прямоугольный треугольник \(ABC\) (\(\angle C=90^\circ\)), \(AB=20\). Пусть \(O\) – центр вписанной в него окружности. Пусть также \(A_1, B_1, C_1\) – точки касания на сторонах \(BC, AC, AB\) соответственно.

Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \[AC_1=AB_1=x; \qquad BC_1=BA_1=y; \qquad CA_1=CB_1.\]

Заметим также, что радиусы \(OB_1\) и \(OA_1\) перпендикулярны \(AC\) и \(BC\) соответственно (как радиусы, проведенные в точку касания). Следовательно, \(CB_1OA_1\) – прямоугольник (четырехугольник, имеющий три прямых угла). Но т.к. его смежные стороны равны, то это – квадрат. Следовательно, \(CA_1=CB_1=4\).

Тогда периметр треугольника равен:

\[AB+BC+CA=(x+y)+(y+4)+(4+x)=2(x+y)+4+4=2\cdot 20+8=48.\]

Ответ: 48

Пусть \(O\) – центр окружности.

\(OA=5\sqrt2\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).

Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=45^\circ\). Тогда прямоугольный \(\triangle ABO\) является равнобедренным, то есть \(AB=OA=5\sqrt2\). Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(BC=AB=5\sqrt2\). Следовательно, по теореме Пифагора

\[AC=\sqrt{AB^2+BC^2}=\sqrt{2AB^2}=AB\cdot \sqrt2=5\sqrt2\cdot \sqrt2=10.\]

Ответ: 10

Пусть \(O\) – центр окружности.

\(OA=10\sqrt2\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).

Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=45^\circ\). Тогда прямоугольный \(\triangle ABO\) является равнобедренным, то есть \(AB=OA=10\sqrt2\). Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(BC=AB=10\sqrt2\). Следовательно, площадь прямоугольного треугольника \(ABC\) равна

\[S_{\triangle ABC}=\dfrac12\cdot AB\cdot BC=\dfrac12\cdot 10\sqrt2\cdot 10\sqrt2= 100.\]

Ответ: 100

Обозначим одну из точек касания окружности и сторон угла за \(A\). Пусть также \(O\) – центр окружности. То есть необходимо найти \(OB\).

\(OA=\sqrt2\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).

Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=45^\circ\). Тогда прямоугольный \(\triangle ABO\) является равнобедренным, то есть \(AB=OA=\sqrt2\). По теореме Пифагора:

\[OB=\sqrt{OA^2+AB^2}=\sqrt{\sqrt2^{\,2}+\sqrt2^{\,2}}=2.\]

Ответ: 2