В треугольнике \(ABC\): \(AF\) и \(BD\) – высоты, \(AF = 4\), \(BD = 3\), \(AC = 6\). Найдите \(BC\).
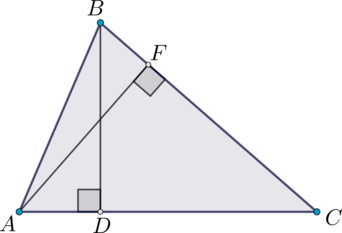
Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию. Так как площадь треугольника не зависит от выбора основания, то \(0,5 \cdot AC \cdot BD = 0,5 \cdot BC \cdot AF\), откуда \(9 = 0,5 \cdot BC \cdot 4\), значит, \(BC = 4,5\).
Ответ: 4,5



